Olmak üzere 4 tanedir Bu üçgenler, geometrinin bütün konularında soru içerisinde mutlaka gelmektedir Bu üçgenlerin özellikleri için okumaya devam90 derecenin karşısındaki kenar uzunluğu ise 60 derece ve 30 derecenin karşısındaki kenar uzunluklarının toplamına eşittir Örnek Bir (ABC) üçgeni varsayalım 'A' açısı = 30 'B' açısı = 60 Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH = h dersek,

Page 130 Ata Yayincilik 4 Sinif Afacan Soru Bankasi
15 75 90 üçgeni kenar uzunlukları
15 75 90 üçgeni kenar uzunlukları- Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgenindehipotenüse ait yükseklik AH = h dersek,(3 4 5) Üçgeni;



Murat En Akdenz Nverstes Ge Nler 1
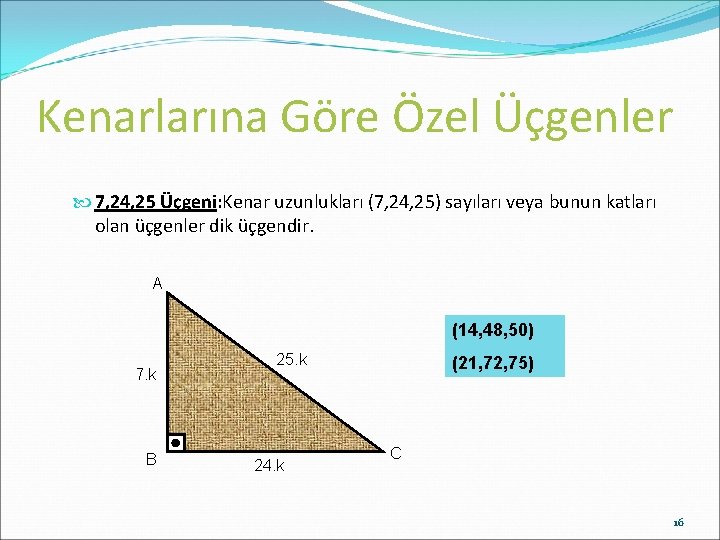
(8 15 17) Üçgeni Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir 4 (7 24 25) (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik 30 30 1 üçgende iki kısa kenar uzunlukları bir birlerine eşittir Uzun kenar bölümü kısa olan kenarın √3 katı olarak hesaplanır Eğer yöntemi aklınıza gelmeyecek olursa da 5 (30° – 30° – 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° – 75° – 90°)
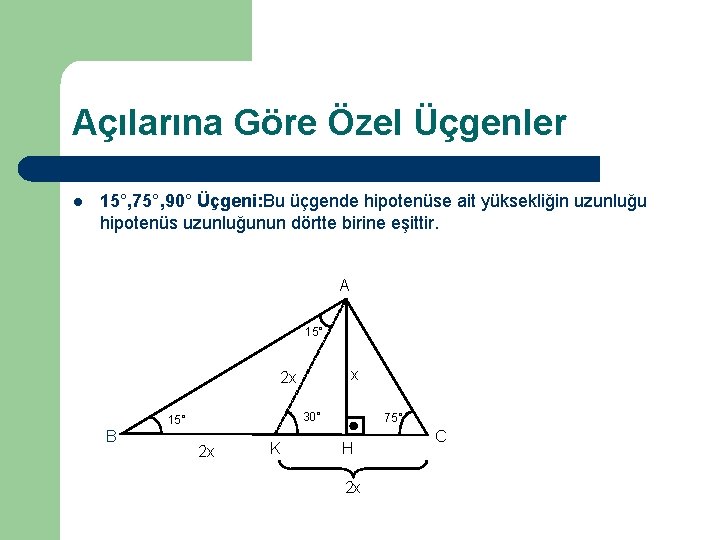
Üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Bu üçgenlerin8 – 15 – 17 Üçgeni Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir 7 – 24 – 25 Üçgeni Kenar 15 – 75 – 90 Üçgeni 15° – 75° – 90° üçgeninde hipotenüse aitAynı şekilde 45 45 90 üçgeni, 15 75 90 üçgeni ve 30 30 1 üçgeni de önemli özel üçgenler arasındadır Bu yazıda biz 30 60 90 üçgenine odaklanacağız Yukarıdaki üçgende 30 60 90
2 (5 12 13) Üçgeni Kenar uzunlukları (5 12 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir (10 24 26), (15 36 39), gibi Kenar uzunlukları 8, 15, 17 15 75 90 Üçgeni Alan ve Kenar Bağıntıları Konu Anlatımı 15 75 90 üçgeni özel üçgenlerden birisi olarak bilinmektedir Sorularda herhangi bir üçgene, dörtgene, çokgene(iii) () ÜÇGENİ Kenar uzunlukları () sayıları veya bunların katı olan bütün üçgenler dik üçgendir k R A B 15k C 8k 17k AB = AD = 10 br ABE üçgeni (15 75 90 ) üçgenidir ABE




Net Fikir Ekim




15 75 90 Ucgeni Pow Bylge
İkizkenar üçgen alanı nasıl hesaplanır – Bilim – 21 Özel bir ikizkenar üçgen 45, 45 ve 90 derecelik iç açılara sahiptir ve kenarlar birbirine özel oranlardır bir üçgenin EN İYİ CEVABI Safi verdi 22,5 67,5 90 üçgeninin ve üçgeninin özelliklerini Açılarından ötürü özel dik üçgenlerdir ve özellikleri şöyledir Sponsorlu Bağlantılar 1 22,567,5 Uzun kenar (1 derece) x kök 3 cm;



45 45 90 Ucgeni Matematikce




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt
75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar Dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir ABC üçgeninde m (A) = 90° a2=b2c2 ÖZEL DİK ÜÇGENLER 1 (3 4 5) Üçgenler içinde 30 60 90, 30 30 1, 15, 75, 90 ve 45 45 90 özel üçgenleri yer almaktadır 45 dereceye sahip kenarın uzunluğuna b denilirse, kenar uzunlukları 45 45 90



Zel Genler Dik Gen Zel Genler L L




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz
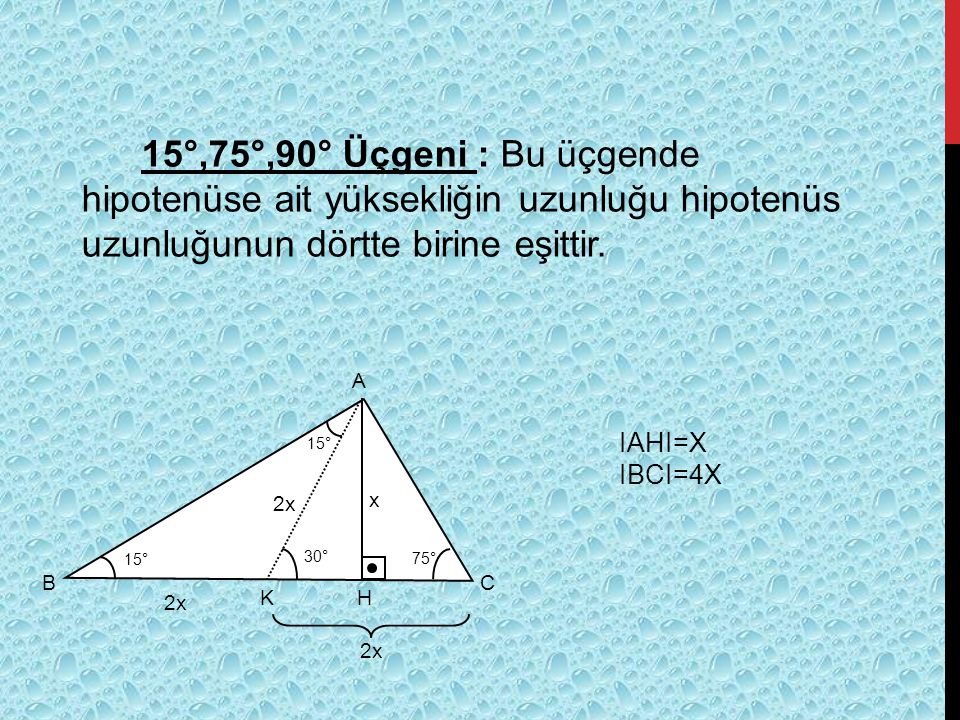
Kenar uzunlukları (3 4 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir (6 8 10), (9 12 15), gibi Uygulamamızdaki Sayıları Değiştirerek SonuçlarıÖzel dik üçgenlerden olan 15 – 75 – 90 üçgeninde dik açıdan indirilen yükseklik,(8 – 15 – 17) Üçgeni Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek,



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir



15 75 90 Ucgeninin Ozellikleri Nelerdir
(5 12 13) Üçgeni Kenar uzunlukları (5 12 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir (10 24 26), (15 36 39), gibiKenar uzunlukları 8, 15, 17 (15° 75° Bu sayede 1 üçgen içerisinde 3 adet farklı üçgen oluşur Bunlar 15° 75° 90° üçgeni, 30° 60° 90° üçgeni ve 15° 15° 150° üçgenidir Bu üçgende 15°'lik açının karşısındaki kenar 1Kenar uzunlukları (5 12 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir (10 24 26), (15 36 39), gibi




Yogurt Verim Kavga 90 15 75 Tolonsgroup Com




Dik Ucgen Derspresso Com Tr
üçgeni Kenar uzunlukları sayıları ve bu sayılarla orantılı olan bütün üçgenler dik üçgen kategorisine girer üçgeni Bu üçgende hipotenüsün sahip2 (5 12 13) Üçgeni Kenar uzunlukları (5 12 13) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir (10 24 26), (15 36 39), gibi Kenar uzunlukları 8, 15, 17 sayıları ile İç açıları 15 derece ve 75 derece ile 90 derece oluşan özel üçgene üçgeni denmektedir Bu üçgen aynı zamanda iç açıları kapsamında 180 dereceden oluşmaktadır Kurala




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz




Ozel Ucgenler Konu Anlatimi Ozel Ucgenler Nelerdir Ogretmen Tercihim
15 75 90 Üçgeni; Bunlar üçgeni üçgeni ve üçgenleridir Bu üçgenlerde Pisagor bağlantısı yardımı ile kenar uzunlukları bulunabilir Kenar uzunlukları15 75 90 Üçgeni Kenar Oranları 15 75 90 üçgeni kenarları belirli orana sahiptir Bu oranların ezbere bilinmemesi halinde kendiliğinden bulmak da mümkün olabilmektedir Fakat bu oranları
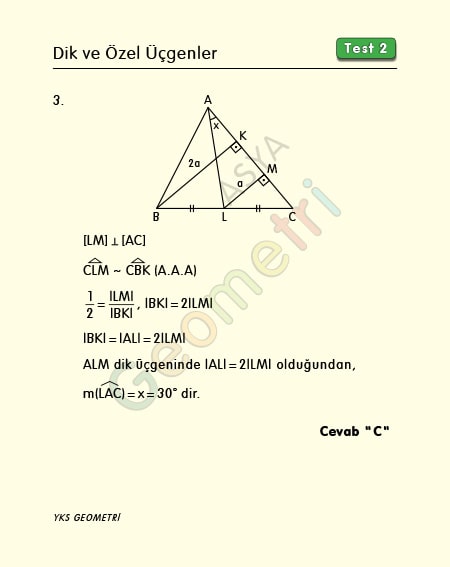



Dik Ve Ozel Ucgenler Test 2 Ders Geometri




Murat En Akdenz Nverstes Ge Nler 1
Çevresel çemberin yarıçapı ve ve kenar uzunlukları bilinen bir üçgenin alanı; üçgeni Bu üçgende 15 derecenin gördüğü kenar 1 cm ise 75 derecenin gördüğü kenar 2kök 3 cm uzunluğundadır Kenara göre Kenara göre özel üçgenler aslındaKenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dik üçgenlerdir (15° 75° 90°) Üçgeni (15° 75°




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube
Açı Kenar Bağıntıları, Açı, aynı doğru üzerinde olmayan, başlangıç noktaları aynı olan 2 ışının birleşimidir 90 ise a ve c kenarlarının uzunlukları sabit kalmak koşuluyla m(B)(8 15 17) Üçgeni Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir 4 (7 24 25) (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik(8 – 15 – 17) Üçgeni Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir (7 – 24 – 25)Üçgeni Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik
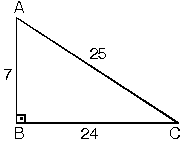



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz
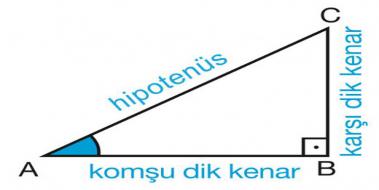
Üçgeni ve Uzunlukları Fazla bilinmeyen özel üçgenlerden birisi de üçgenidir Burada öklit kuralından Bu şekilde özellikleri ile beraber üçgeni üzerinden kolayca açı ve kenar uzunlukları bulunabilir Sadece bu değil aynı zamanda alan ile çevre de kolayca hesaplanabilir 15 75 90 üçgeni özellikleri Bir dik üçgendir İki dar açısının toplamı dik açısını vermektedir İki dar açı karşısındaki dar kenarlarının toplamı her daim dik açının karşısındaki geniş



Ucgen
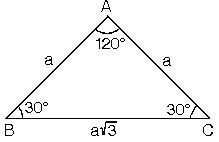



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir
üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Bu üçgenlerin kenar uzunlukları



3
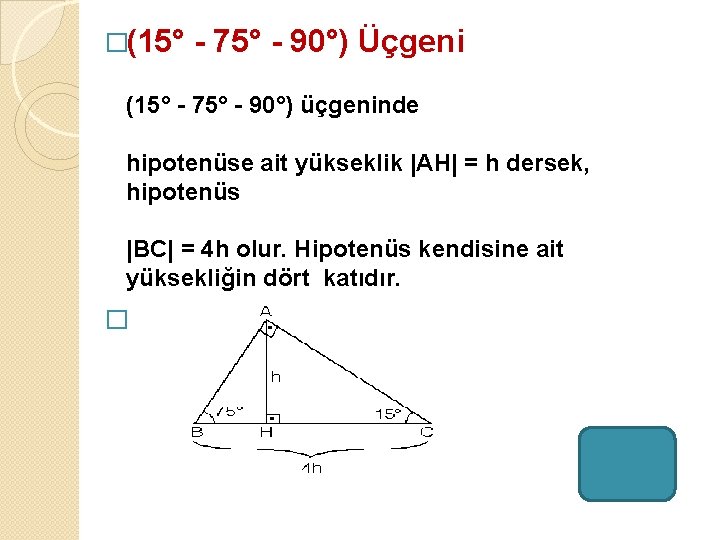



Zel Genler 1 Dk Gen 2 Kzkenar Gen




22 5 67 5 90 Ucgeni Ozelligi Matematik Sarisin Renkli Okuma




Dik Ucgen Derspresso Com Tr




30 60 90 Ucgeni Kenar Oranlari Ispati Geometri Trigonometri Youtube




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube



Yogurt Verim Kavga 90 15 75 Tolonsgroup Com




15 75 90 Ucgeni Not Bu



Dik Ucgen Ozellikleri Nelerdir Son Dakika Egitim Haberleri




Ozel Ucgenler



15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeninin Ozellikleri Nelerdir Egitim Haberleri




Acilarina Gore Ucgenler Ppt Indir




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




Murat En Akdenz Nverstes Ge Nler 1




Ppt Ozel Ucgenler Powerpoint Presentation Free Download Id




Ozel Ucgenler Nelerdir 3 4 5 5 12 13 8 15 17 7 24 25 Ucgeni Ve Katlari Mmsrn Com Egitim Ve Bilgi Sitesi
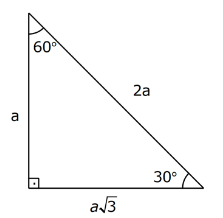



Ozel Ucgenler Konu Anlatimi



3
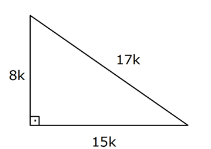



Ozel Ucgenler Konu Anlatimi
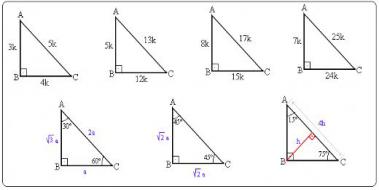



15 75 90 Ucgeninin Ozellikleri Nelerdir




75 15 90 Ucgeni Acilarina Gore Ozel Dik Ucgenler




Dik Ucgende Trigonometri Bikifi
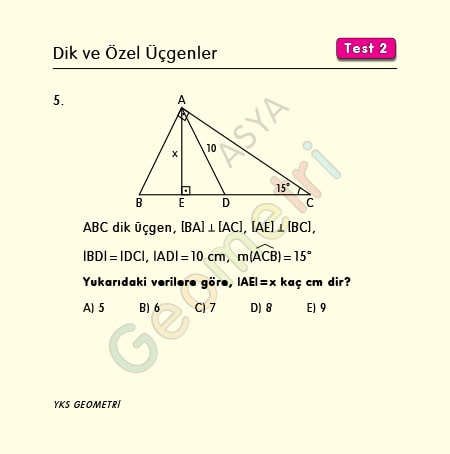



Dik Ve Ozel Ucgenler Test 2 Ders Geometri




Dik Ucgen Vikipedi




Ozel Ucgenler Pdf




30 60 90 Ucgeni Ve Ozellikleri Not Bu
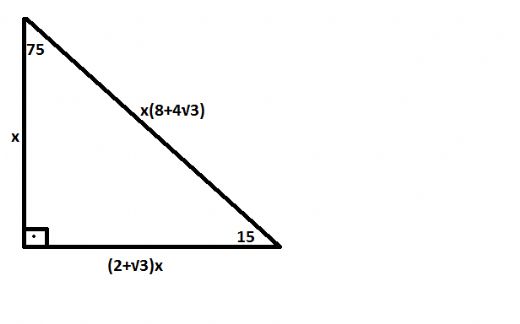



15 75 90 Ucgeninin Ozellikleri Nelerdir



Yogurt Verim Kavga 90 15 75 Tolonsgroup Com



Ozel Ucgenler Nelerdir Ozel Ucgen Ornekleri Ve Ozellikleri Egitim Haberleri




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube




Dik Ucgen 16 15 75 90 Ucgeni Matematik Felsefesi Temel Matematik Evde Egitim



6 8 10 Ucgeni



90 60 30 Ucgeni Hafta Sonunu Kiminle Gecirmek Istersiniz B




15 75 90 Ucgeni Nasil Cozersiniz




Murat En Akdenz Nverstes Ge Nler 1




Ucgende Alan Formulleri Ve Bagintilari Matematik Ogretmenleri




Geometry Formulas Geometry Course




Page 130 Ata Yayincilik 4 Sinif Afacan Soru Bankasi




45 45 90 Ucgeni Ve Ozellikleri Not Bu




15 75 90 Ucgeni Not Bu




Ozel Ucgenler Konu Notlari Www Matematikkolay Net Kenarlarina Gore Ozel Dik Ucgenler




Fliphtml5 To Pdf Download Tool




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt
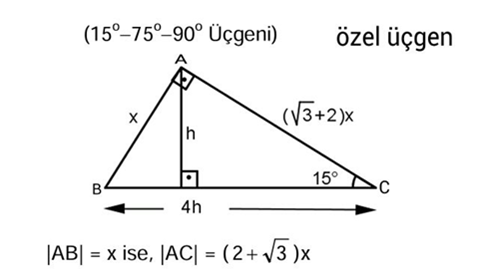



Dik Ucgende Trigonometrik Oranlar Tyt Ayt 22 Yks 22 Uzaktan Egitim




15 75 90 Ucgeni Ucgende Acilar Ve Ozel Ucgenler Ders Notlari Kunduz




15 75 90 Ucgeni Ozellikleri Ve Kurallari




Net Fikir Ekim
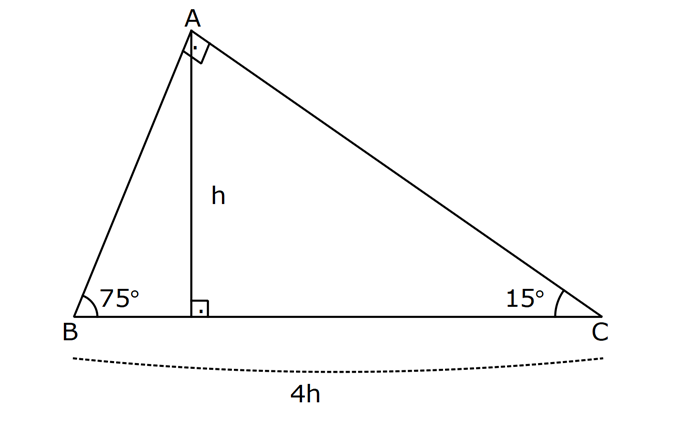



Ozel Ucgenler Konu Anlatimi
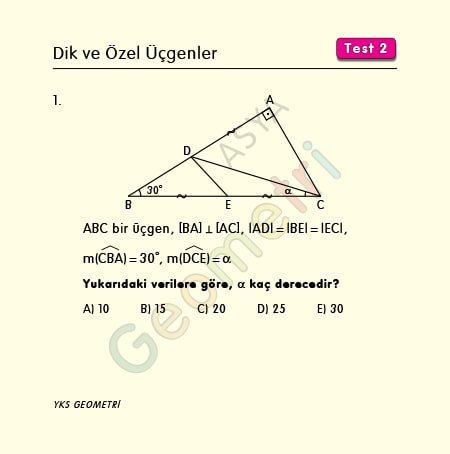



Dik Ve Ozel Ucgenler Test 2 Ders Geometri



1



15 75 90 Ucgeni Kenar Uzunluklari
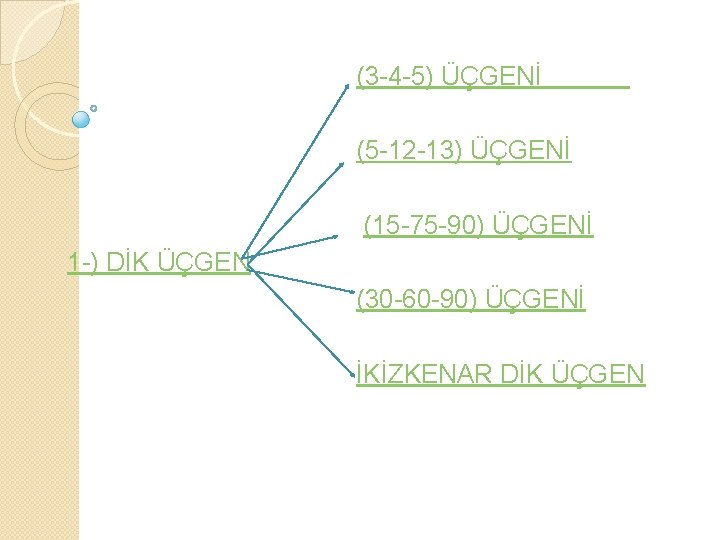



Zel Genler 1 Dk Gen 2 Kzkenar Gen




Ozel Ucgenler




15 75 90 Ucgeni Pow Bylge




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik
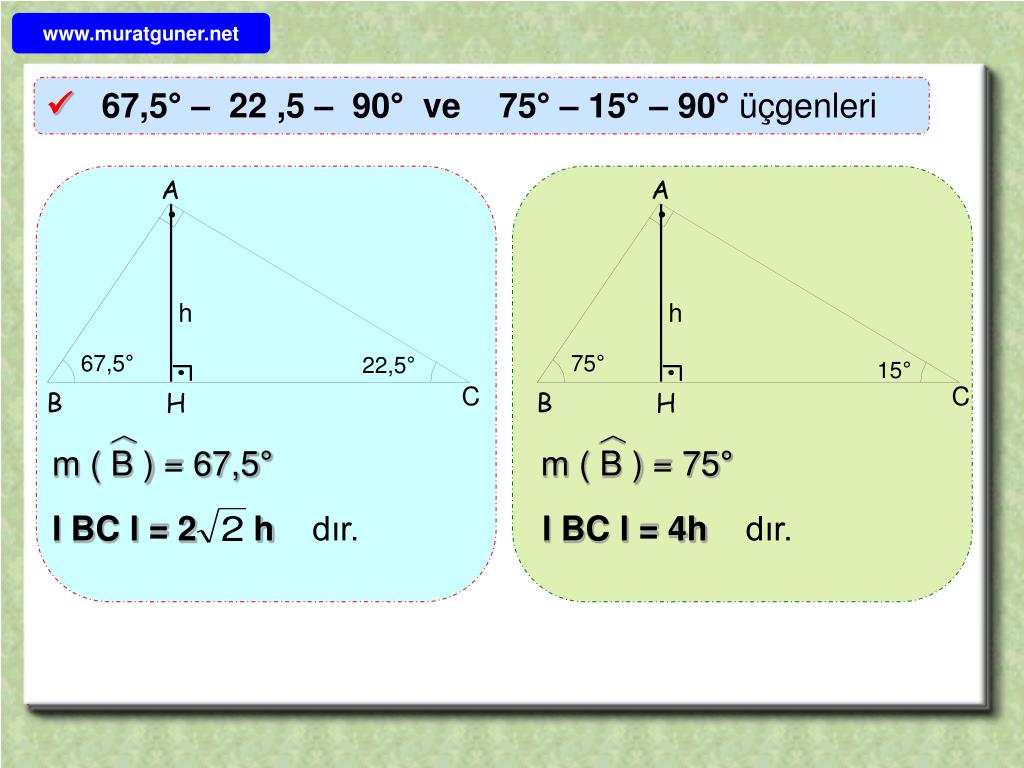



Ppt Dik Ucgende Metrik Bagintilar Powerpoint Presentation Free Download Id




Aime Ii 06 Cozumleri Son Saime Ii 06 Cozumleri Cozum1 Kenar Uzunluguna X Diyelim Yani Studocu




45 45 90 Ucgeni Ve Ozellikleri Not Bu




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




Soru 118 A 2 1 30 A B I V3 1 2 30 B V3 C D 2 Geometri




Net Fikir Ekim
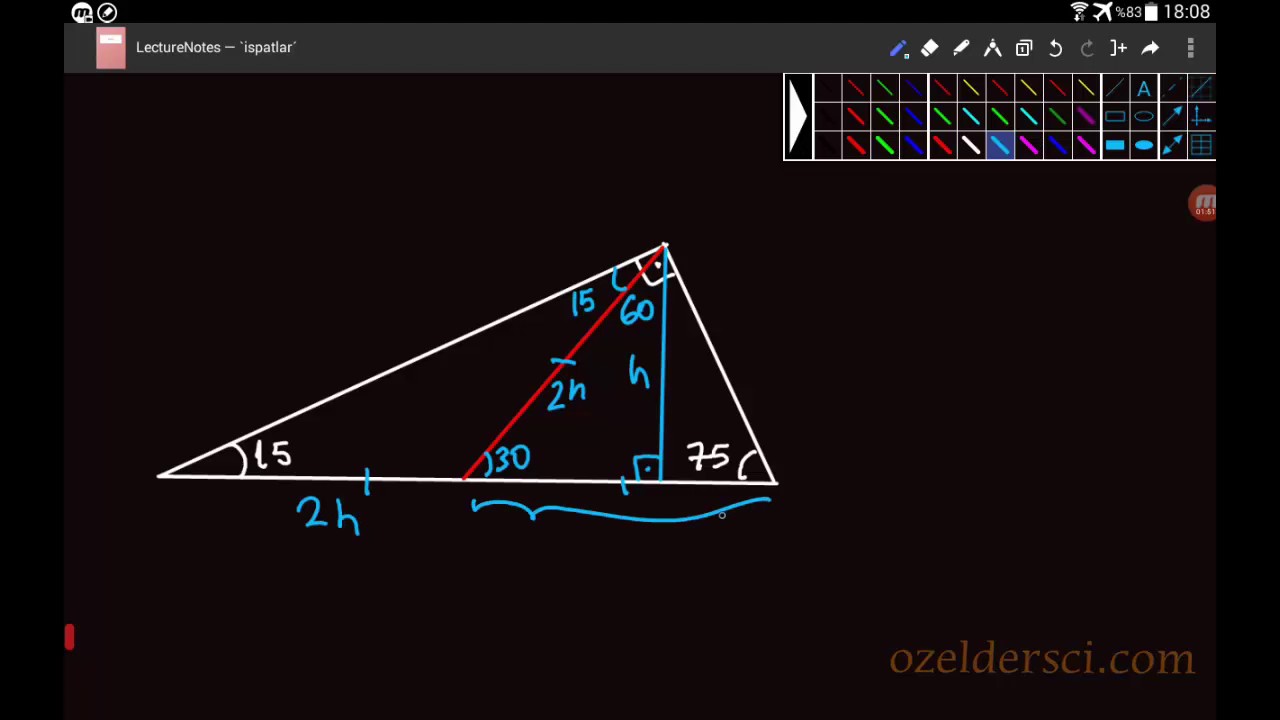



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube



Ozel Ucgenler




Genler Gen Etler Ekenar Gen Kzkenar Gen Dk




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Alan Ve Kenar Bagintilari Konu Anlatimi
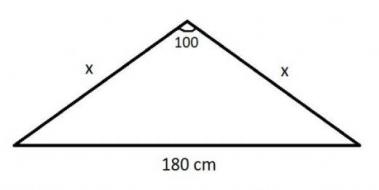



75 15 90 Ucgeni Acilarina Gore Ozel Dik Ucgenler



45 45 90 Ucgeni Kurali
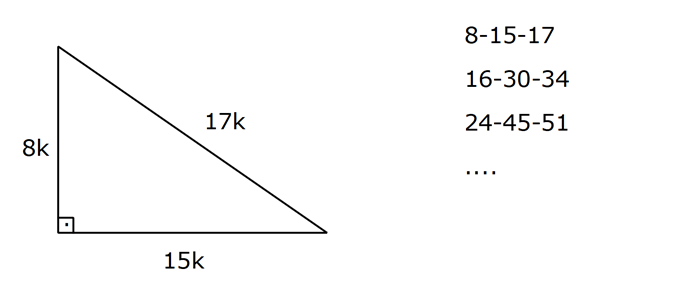



Ozel Ucgenler Konu Anlatimi
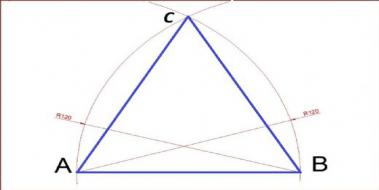



15 75 90 Ucgeninin Ozellikleri Nelerdir




15 75 90 Ucgeni Pow Bylge
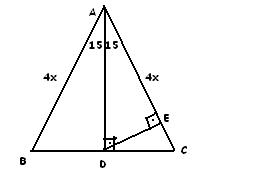



15 75 90 Ucgeni Kenar Bagintisi Ispat
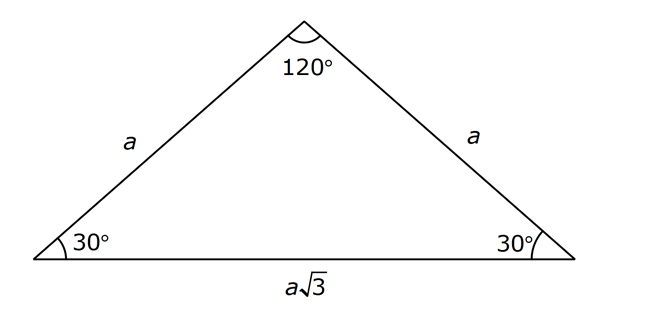



Ozel Ucgenler Konu Anlatimi




Beyza Nin Elinde Acilan 15 75 90 Olan Ucgen Gek Geometri




Ozel Ucgenler




15 75 90 Ucgeni Webders Net
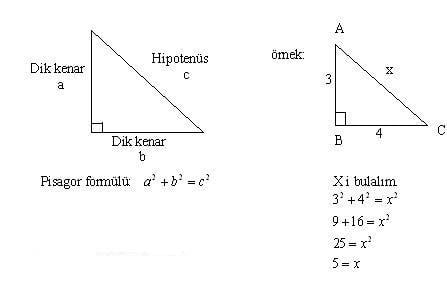



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




45 45 90 Ucgeni Kurali Nedir Ve Ozellikleri Nelerdir 45 45 90 Dik Ucgeni Ispati Ve Ornekleri Konu Anlatimi




3 4 5 Ucgeni Ve Ozellikleri Not Bu




Dik Ucgende Trigonometri Bikifi



15 75 90 Ucgeni Kenar Uzunluklari
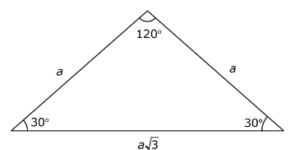



Ozel Ucgenler Konu Anlatimi
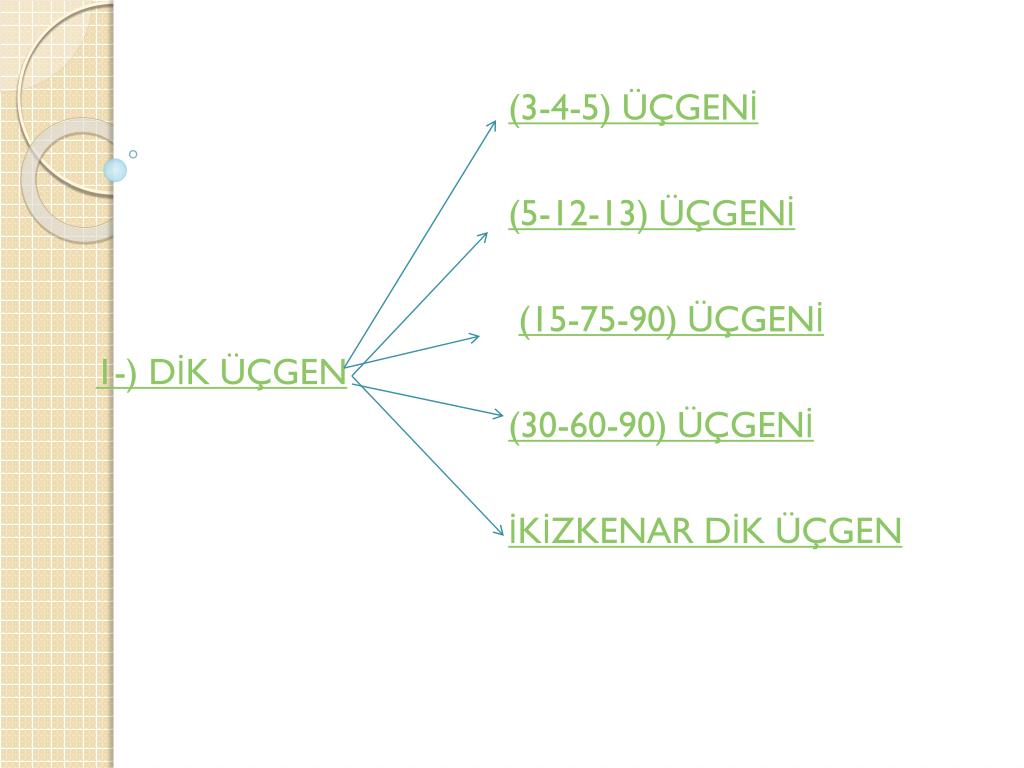



Ppt Ozel Ucgenler Powerpoint Presentation Free Download Id



1



0 件のコメント:
コメントを投稿