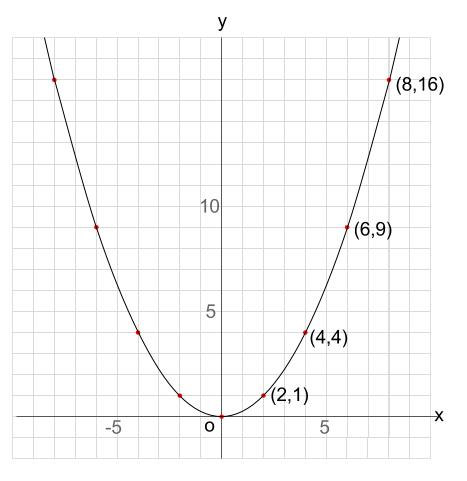
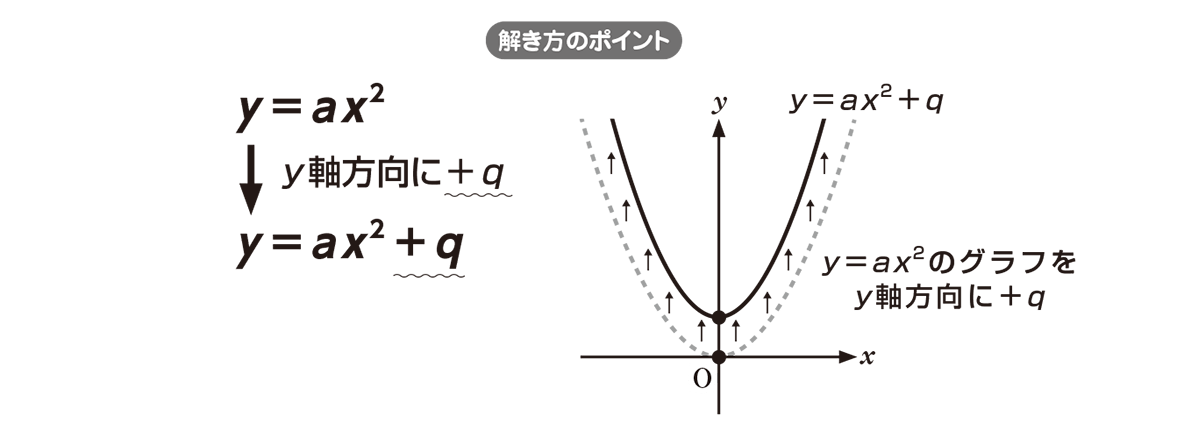
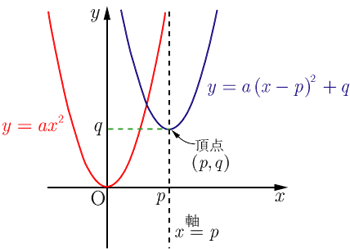
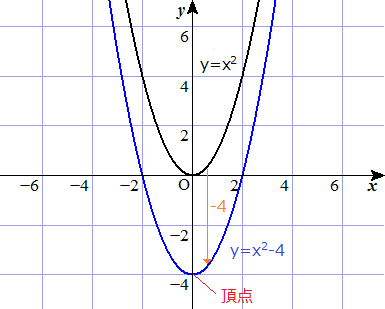
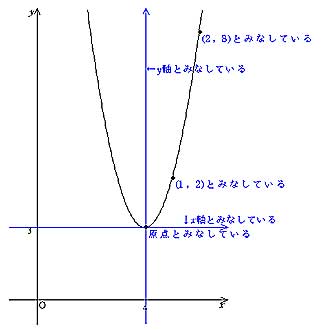
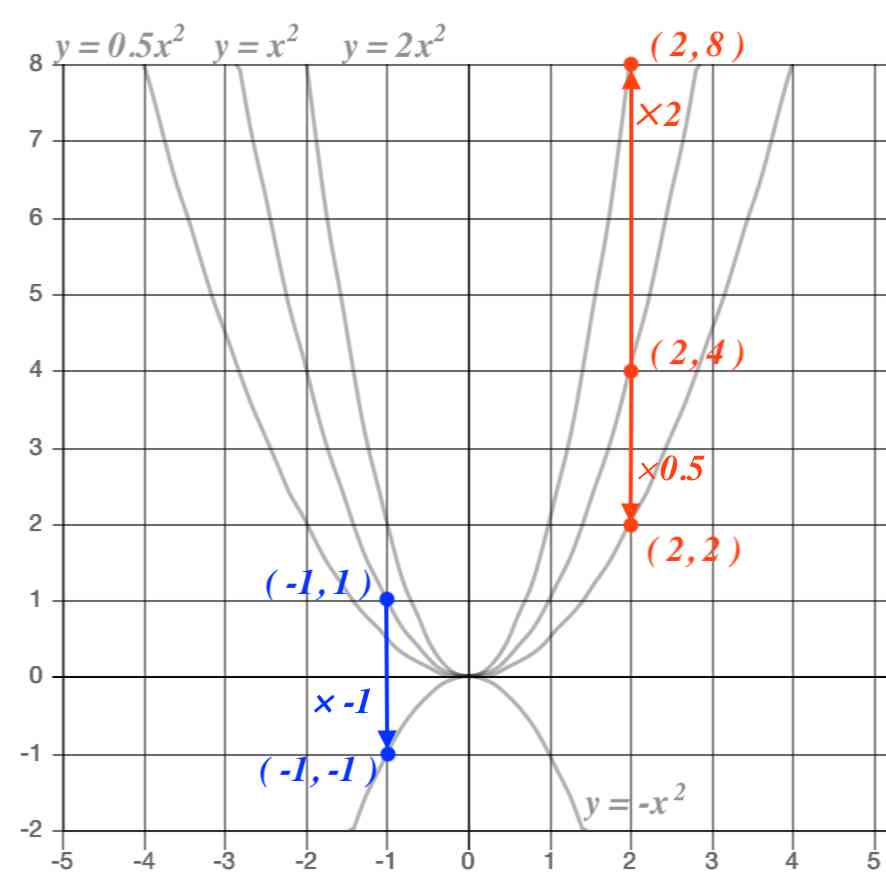
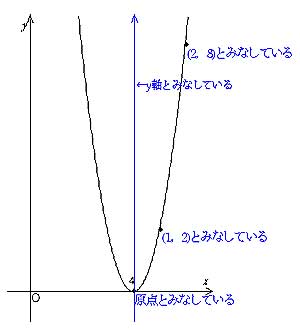
入力x,出力yとが直線関係にあれば次式で表される。 ここで, a, b は任意の定数である。 n 組の測定データ: 最も良く当てはまる直線は, y i と ax i b との差の2乗の和が 最小となる a と b の場合である。 y ax b 2)最小二乗法の計算 1 1 2 2 x y x y $y=ax^2q$ のグラフは、 $y=ax^2$ のグラフを y 軸方向に q だけ移動したものである 基本二次関数 y=ax^2 のグラフ では、放物線の頂点と軸の紹介をしました。 グラフの読み取り \(2\) 乗に比例(\(2\) 次関数)のグラフを読みとることも、非常に重要です。 例題1 下の図の放物線の式を求めなさい。 解答 原点を通る放物線なので、 放物線の式は \(y=ax^2\) となり

中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく
Y=ax二乗のグラフ
Y=ax二乗のグラフ-図の放物線lはy= 1 2 x 2 の グラフで、放物線mはy=ax 2 のグラフである。lとmがx軸に平行な直線nと交わる点をそれぞれA, Bとする。Aのx座標が4, Bのx座標が2のとき、aの値を求めよ。 A B l m n x y O 2 4 図の放物線lはy=ax 2, 放物線mはy= 1 8 x 2 のグラフである。下のグラフが\(y=3x^{2}\)です。 一方、下のグラフが\(y=3x^{2}\)です。 このように、係数\(a\)が正のときは上が開いた形に、負のときは下が開いた形となります。 より詳しく知りたい方は→中3数学y=ax^2のグラフってどんな形になるの?いくつかの特徴につい



中学数学 Y Ax 2 のグラフを読み取る 中学数学の無料オンライン学習サイトchu Su
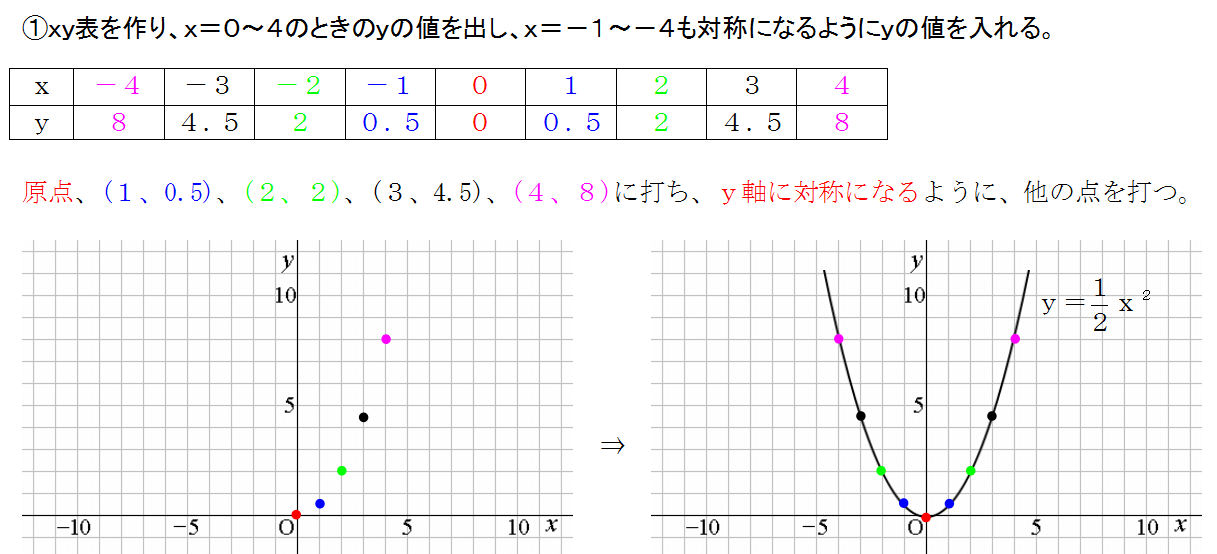
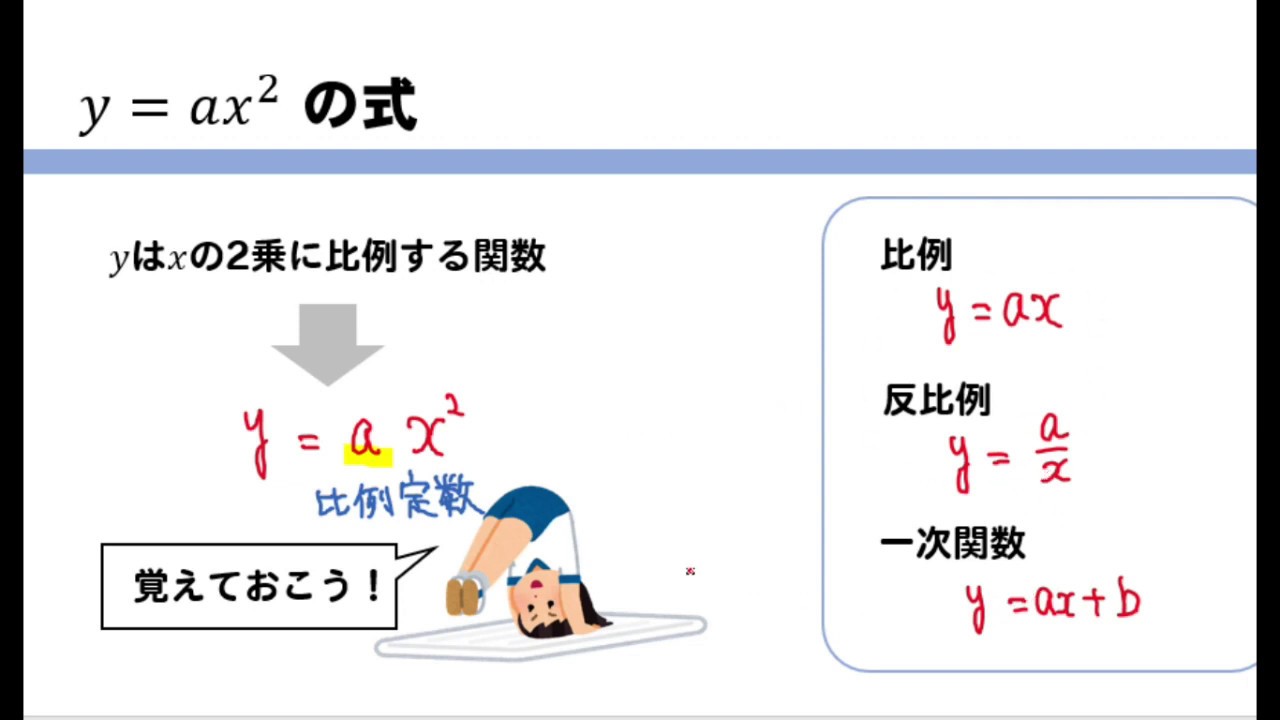
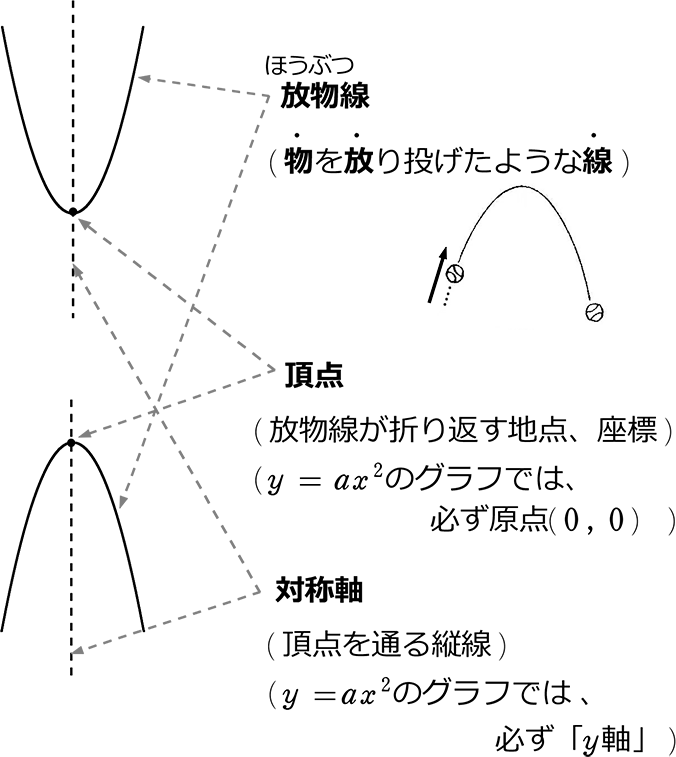
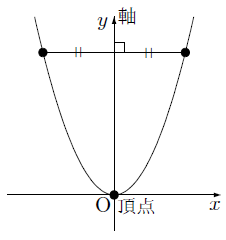
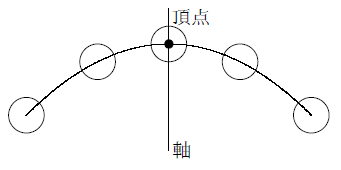
となるから, y=ax2 のグラフは 軸に関して対称であるといえます。 したがって, y軸は放物線 =ax2 の軸(対称軸)とよばれます。な お,一般に放物線とその軸との交点を頂点といい,y=ax2 のグラフ では原点が頂点となります。LINEST関数による最小二乗法の計算 Excelには、最小二乗法による直線フィッティング用にLINESTという関数が用意されています。 一般的な使い方は =LINEST(計算に使うYの範囲、計算に使うXの範囲、Y切片を0にするかしないか) というような形式です。 X,Yという順番ではなく、Y,Xという順番であることに注意してください。 範囲の指定の方法ですが という表があり 関数y=ax2乗放物線グラフの書き方はこれでバッチリ! yはxの2乗に比例する関数 関数グラフ上の平行四辺形の座標、面積、二等分線などの問題を解説!
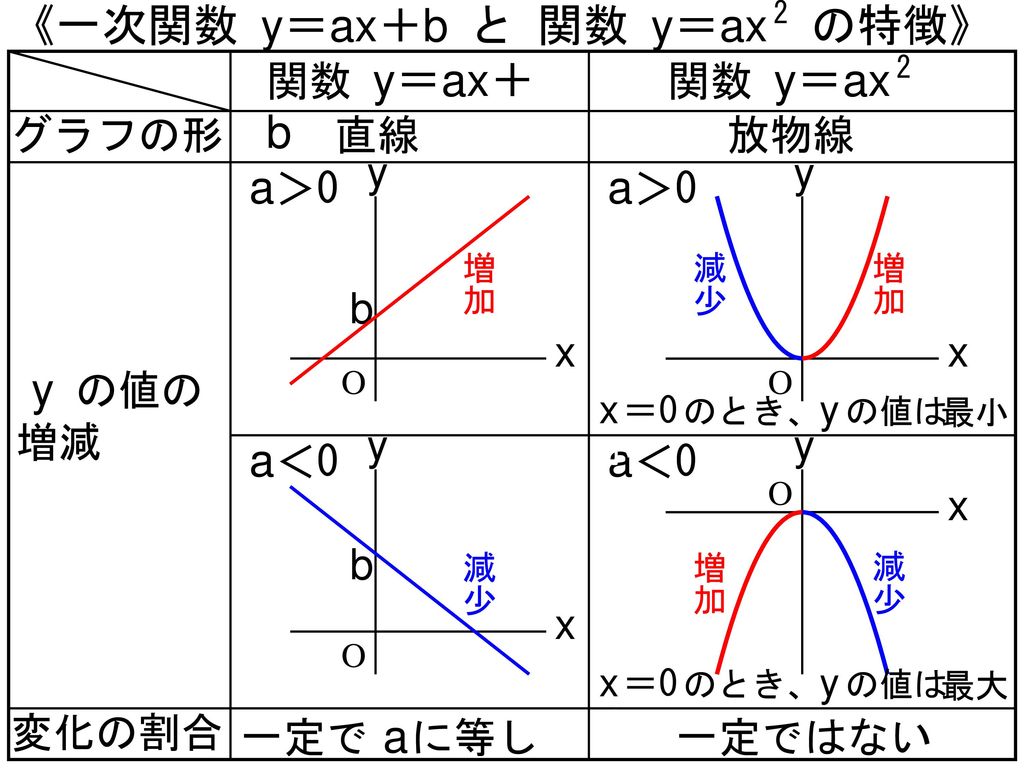
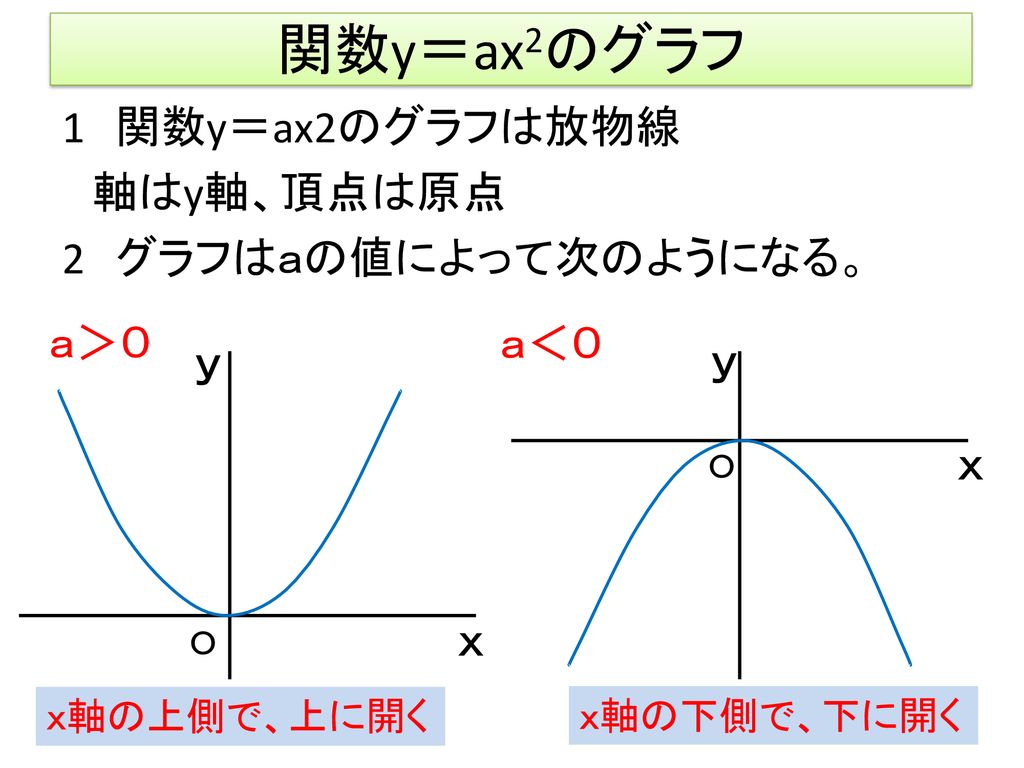
・y=ax2 のグラフの 特徴を見つけ,a の値との関係を 考える。 関数y=ax2 のグ ラフの特徴を調 べ,グラフをかこ うとしている。 a の値の変化と グラフの形を関 連付けて調べ, グラフの特徴を 放物線や軸,頂 点の意味と関数 y=ax2 のグラフ の特徴を理解し関数 y=ax 2 のグラフ(3) 関数 y=ax 2 のグラフ(4) 変域とグラフ(1) 変域とグラフ(2) 変域の割合(1) 変域の割合(2) 変域の割合(3)2次関数y=xの2乗+ax+bのグラフをx軸方向に-1、y軸方向に2だけ 平行移動すると頂点の座標が(-2,6)になるように、定数a、bの値を 求めよ!をどうか今日中にお願いします 質問<1347>りさぴょん「最小値が与えられた二次関数」
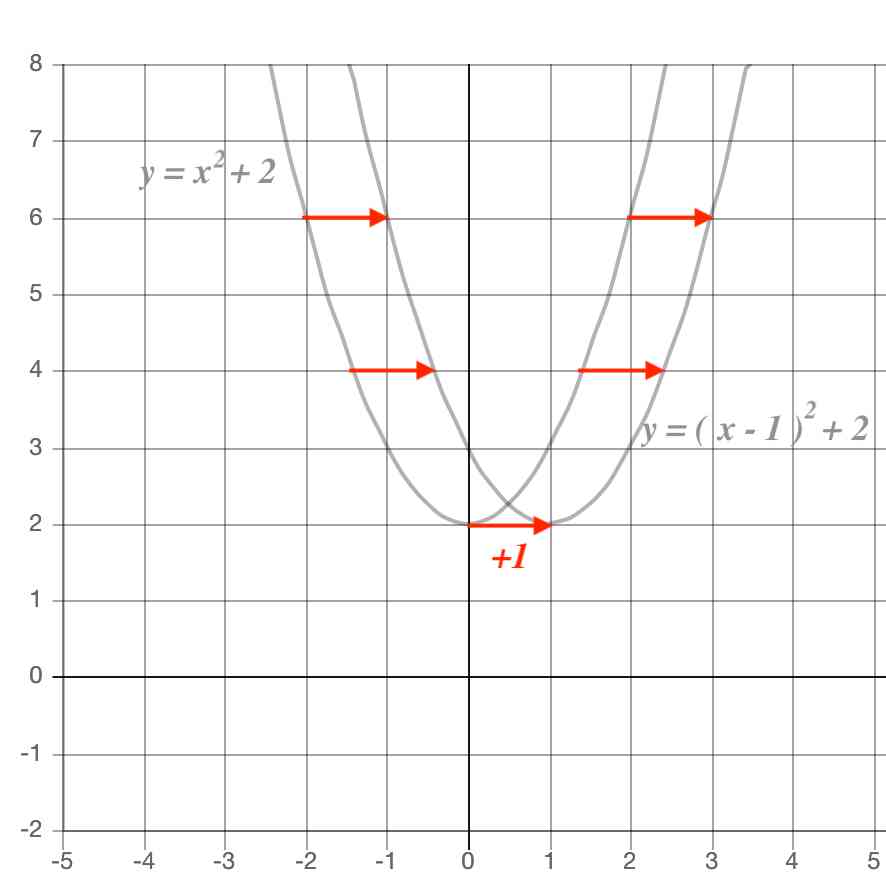
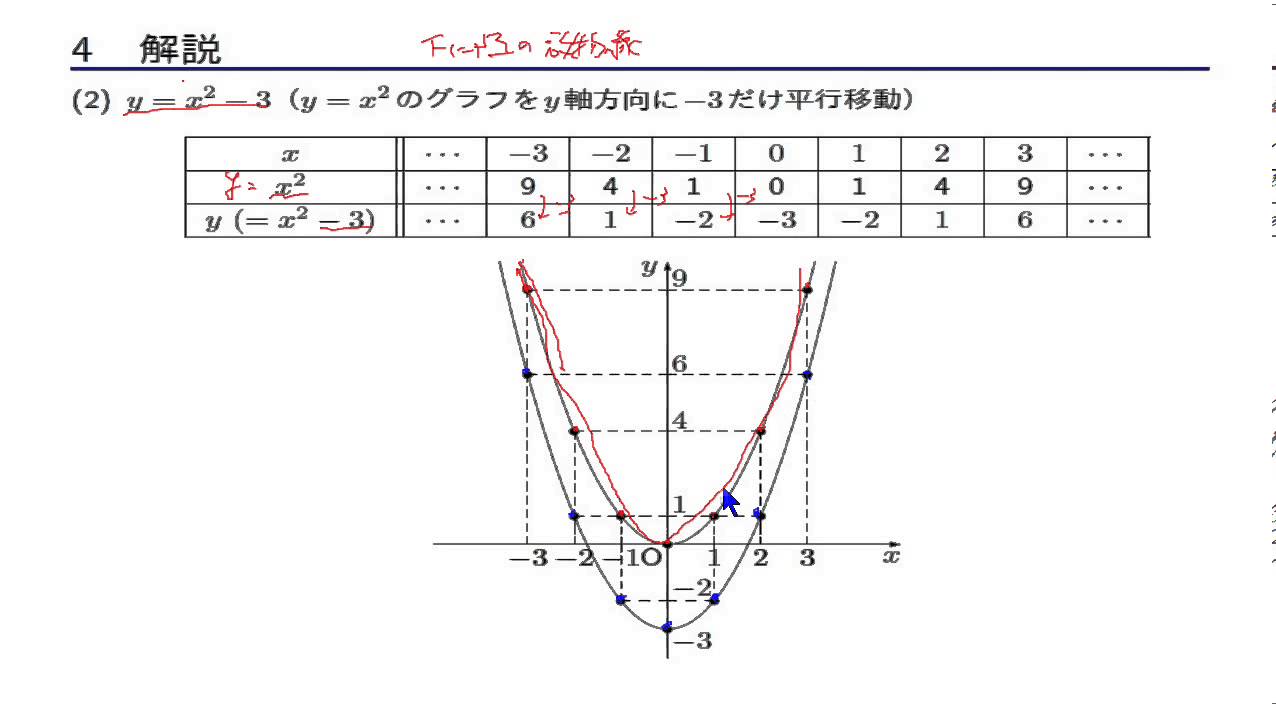
・y=ax 2 q のグラフ ↓ →例題 ↓ y=ax 2 q のグラフ y=ax 2 q のグラフを y=ax 2 のグラフと比較しながら考えてみます。 やはり表を作ってみることが大切です。 下の表は 2x 2 と 2x 2 1 を比較したものです。 xのどの値においても, 2x 2 1 の値は 2x 2 の値に1を足したものです。 したがって, yY = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味,関数 y = ax2 y = a x 2 のグラフの特徴,直線の式の求め方を理解する 本時の目標また,関数y=ax 2 はy軸を対称の軸にして左右対称ですので,2と4で,xの絶対値が大きい方がyの最大値をとることも考えましょう。 試しにx=2とx=4の両方を代入してみましょう。x=2のときはy=4a,x=4のときはy=16aになりますね。



中3数学 関数y ax二乗 放物線と直線1 発展問題 問題 324 プリント




Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト
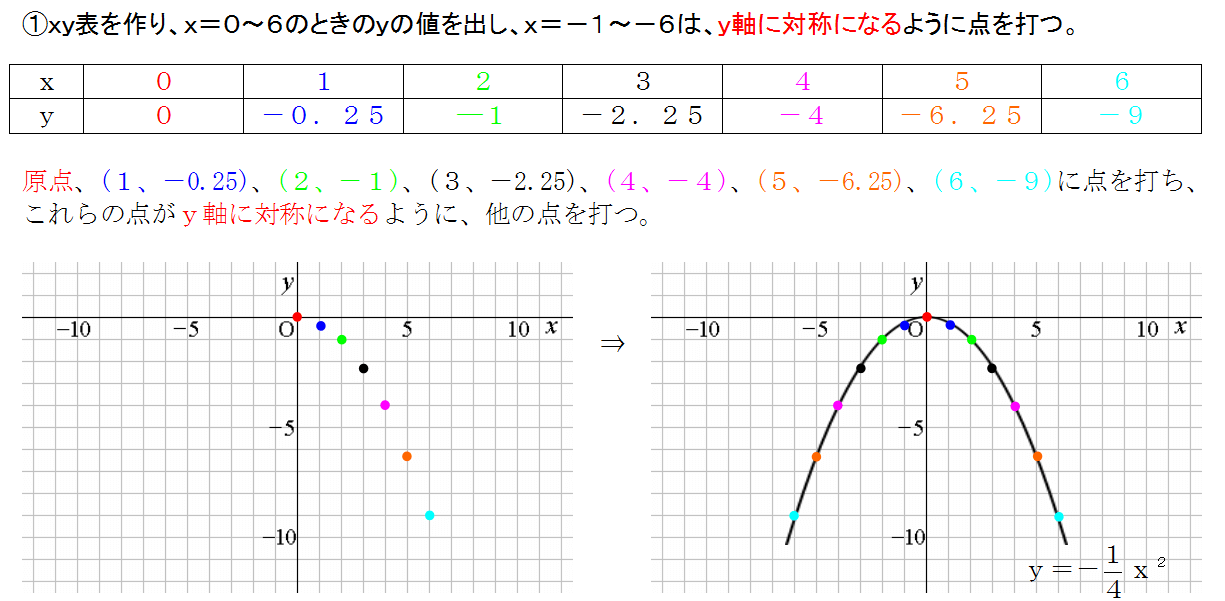
Y = ax2 y = a x 2 2乗に比例 y y が x x の関数であり、 x x と y y の間に y = ax2 y = a x 2 という関係式が成り立つとき、 y y は x x の 2 2 乗に比例する という。 ただし、 a a は 0 0 でない定数で、比例定数といいます。 「 y y は x x の 2 2 乗に比例する」と問題文にY=ax 2 のグラフの特徴 必ず原点を通り、その原点が頂点である。 y軸について対称である。 a > 0のときは上に開き、a < 0のときは下に開く。 aの絶対値が小さいほどグラフの開きが大きい。 y=ax 2 のグラフとy=ax 2 のグラフはx軸について対象である。関数y=ax2の関 係などを,表,式,グ ラフを用いて的確に表 現したり,数学的に処 理したりするなど,技 能を身に付けている。 事象の中には関数y =ax2などとして捉 えられるものがあるこ とや関数y=ax2の 表,式,グラフの関連



高校数学 Y Ax 2 Qのグラフ2 映像授業のtry It トライイット



関数x Ax二乗のxとyの対応表の書き方を教えてください Yahoo 知恵袋
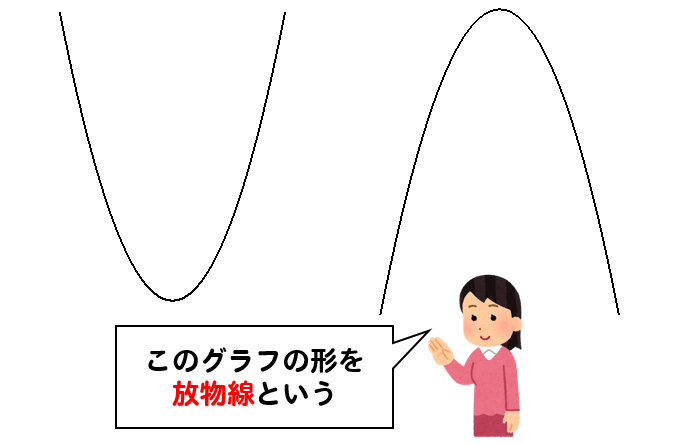
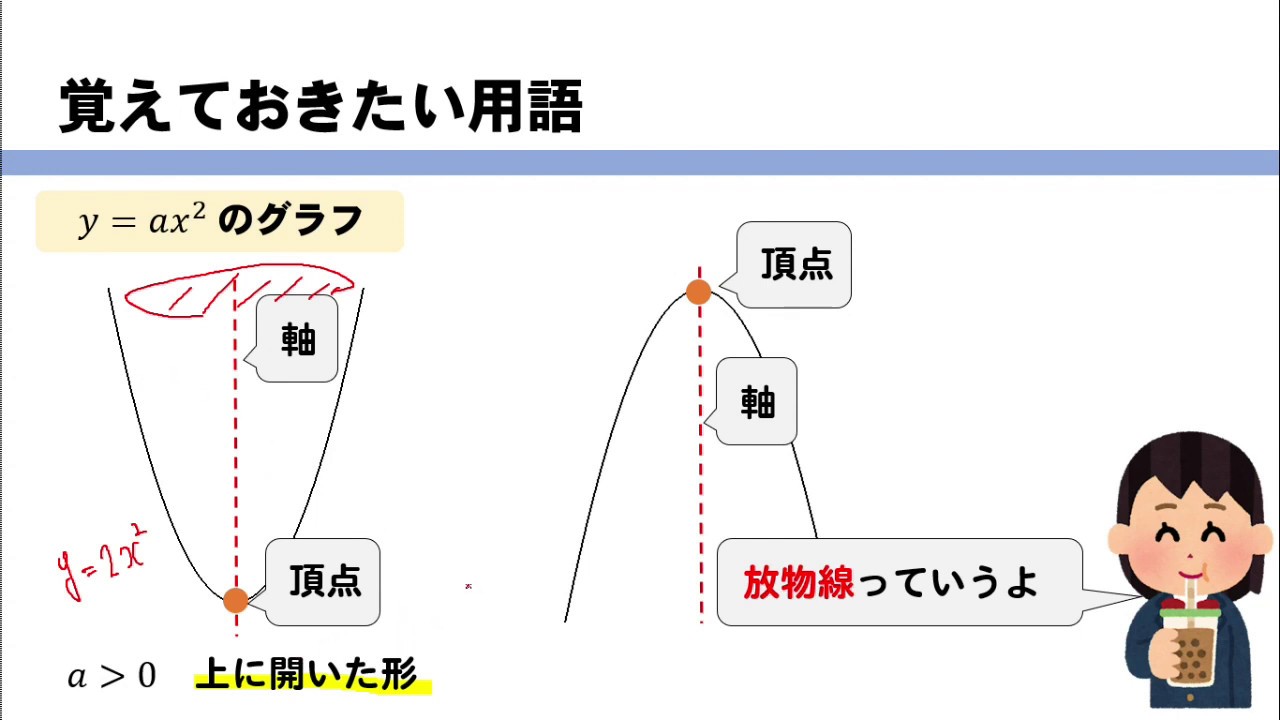
y=ax2乗のグラフで覚えておきたい用語 まず、グラフの形は 放物線 となります。 この放物線は左右対称の形となっており、その折れ目となる線のことを 軸 といいます。・グラフの性質 ・変域の求め方 誤字脱字があったらごめんなさい。 ระดับชั้น Junior High3, Textbook 新編 新しい数学3 東京書籍, Unit 関数y=ax^2, Keyword y=ax二乗Y=ax 2 のグラフを,x 軸方向へ p,y 軸方向へ q だけ平行移動する。 そこで,X=xp,Y=yq とおくと,x=Xp,y=Yq となるので,与式へ代入すると,Yq=a(Xp) 2




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師
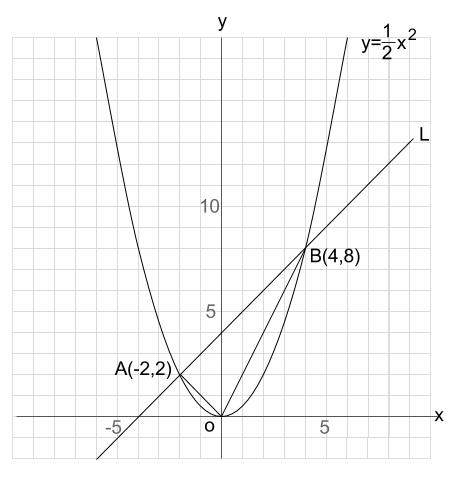
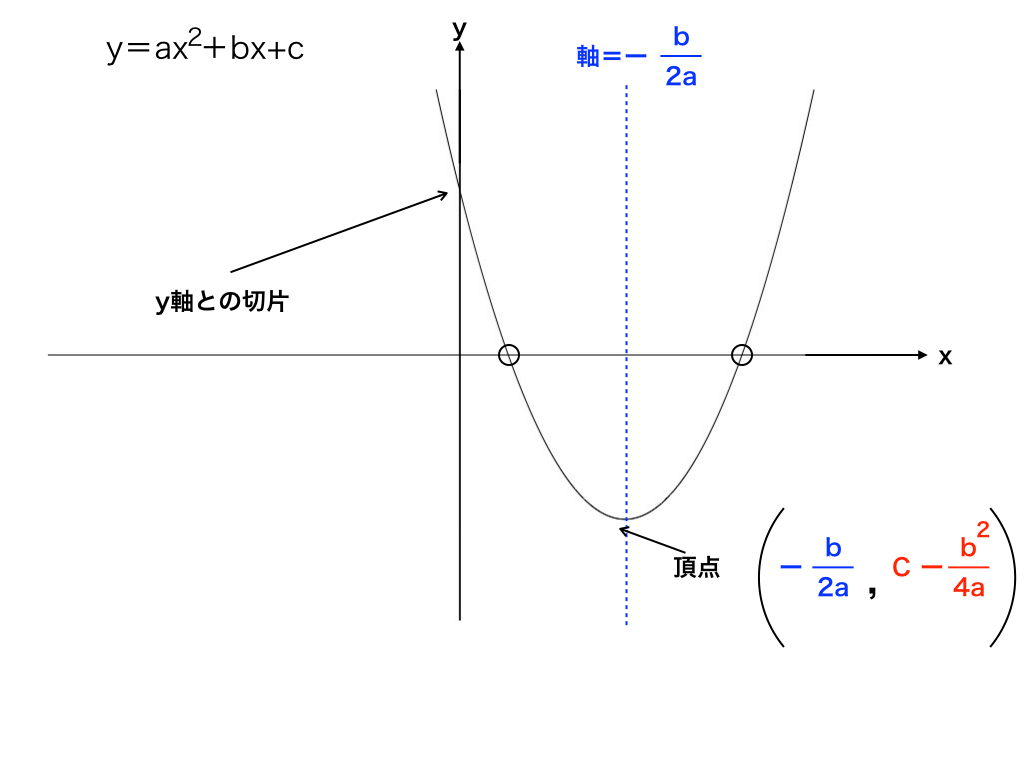
2次関数 $y=ax^2bxc$ のグラフは \begin{align} y=&ax^2bxc\\ =&a\left\{x^2\dfrac{b}{a}x\right\}c\\ &\quad\blacktriangleleft x^2の係数でくくる\\ =&a\left\{\left(x\frac{b}{2a}\right)^2\frac{b^2}{4a^2}\right\}c\\ &\quad\blacktriangleleft 平方完成\\ =&a\left(x\frac{b}{2a}\right)^2\frac{b^2}{4a}c\\ &\quad\blacktriangleleft \{~~\}をはずす\\Aが正のときのy=ax 2 のグラフ 今回はまず、y=ax 2 という式において、a>0のときにグラフがどうなるかを覚えよう。 y=ax 2 (a>0)のグラフは、図のように 「原点を通る、上に開いた放物線」 になるよ。 U字型 のイメージだね。 例題をいっしょに解きながら、実際にグラフが 「原点を通る、上に開いた放物線」 になることを確認していこう。右図のように2次関数 y=ax 2 のグラフと直線 y=bx3 のグラフが2点A,Bで交わり,点Aの座標が (−2, 2) であるとき,次の問いに答えなさい. (1) 定数 a の値を求めなさい. (2) 定数 b の値を求めなさい. (3) 点Bの座標を求めなさい. (4) AOBの面積を求めなさい.



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ
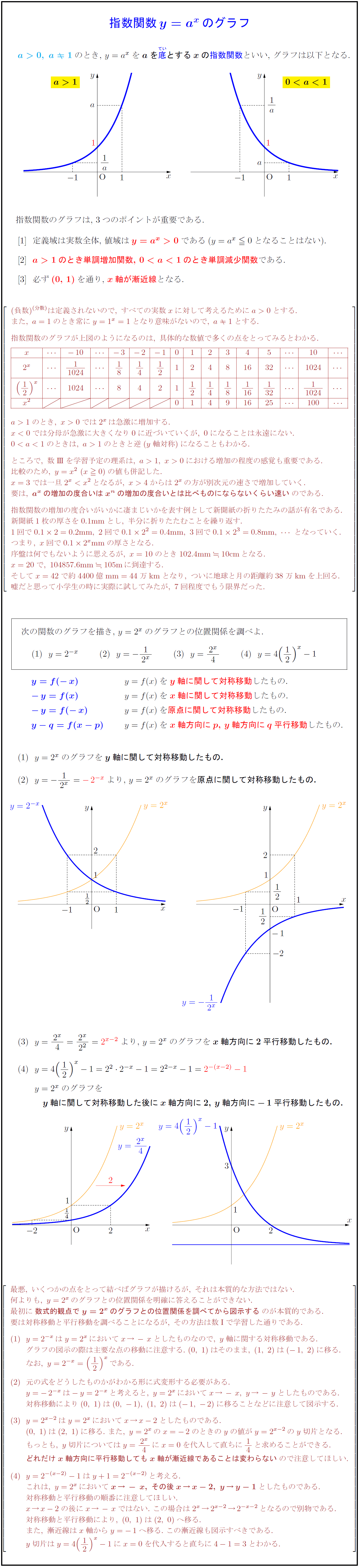
関数グラフ GeoGebra x y z π 7 8 9 ×例:y=x, y=x, y={2^x} グラフの縮小率を大きくすると、広い範囲が見られます。逆に、縮小率を小さくすると、原点付近を拡大できます。 指数関数について y=x 2 ではなくて、y=2 x としてみます。 指数関数と対数関数は対の関係です。関数 関数y =ax2(2) 1 次の各問いに答えなさい。 (1)yはxの2乗に比例し、x=3 のときy =27 である。 ① yをxの式で表しなさい。 ② x=5 のときのyの値を求めなさい。 (2)関数y = ax2で,x=2 のときy = −8である。 ① aの値を求めなさい。 ② x= −4のときのyの値を求めなさい。 (3)yはxの2乗に比例



数学3年 2次関数 Y Ax2 2次関数のグラフ 2次関数の変域 2次関数の応用 2次関数のグラフ Xの2乗に比例する関数 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3 問題4 正解4 解説




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント
Y=ax 2 のグラフ 2次関数とは、y=2x 2 y=ax 2 bxc 中学校では、b=0,c=0 の場合だけ扱い、関数y=ax 2 のグラフが放物線という曲 線になっていることを勉強しました。 ・グラフの性質 ・変域の求め方 誤字脱字があったらごめんなさい。 学年 中学3年生, 教科書 新編 新しい数学3 東京書籍, 単元 関数y=ax^2, キーワード y=ax二乗A,bをy=axbに代入して,y=x4 (答え) y=x4 別解(裏技的?) 関数y=ax 2 上の2つの点B,Cがあるとして,それらのx座標がb,cだったとすると,直線BCの式は y=a(bc)xabc ・・・(*) になるのです。このことも後々で証明しようと思いますが,今は代入して触れるだけで。




Y Ax2乗 グラフの特徴と書き方をイチから解説します 中学数学 理科の学習まとめサイト




二次関数 Wikipedia
\(y=ax^2\)という形をした関数のグラフは このような 放物線 と呼ばれるグラフになります。 放物線というワードは定期テストで問われることもあるから覚えておこう!・学校図書(問い・y= ・グラフ→x,y の関係が比例かどうか?) ・教育出版(問い・グラフ→枚数が100 枚ときに何段?) ・大日本図書(コラムでの説明) 風速x y の風が吹く時の、壁にかかる風圧を パスカルとすると、yはxに2乗に比例する〈変数・風速x と風 圧y〉比例の式 y=ax(aは比例定数) の式を、グラフで表すときのポイントは、次の通りだよ。 POINT 実際にy=2xなどの式がどんなグラフになるか、例題を通して確認しよう。




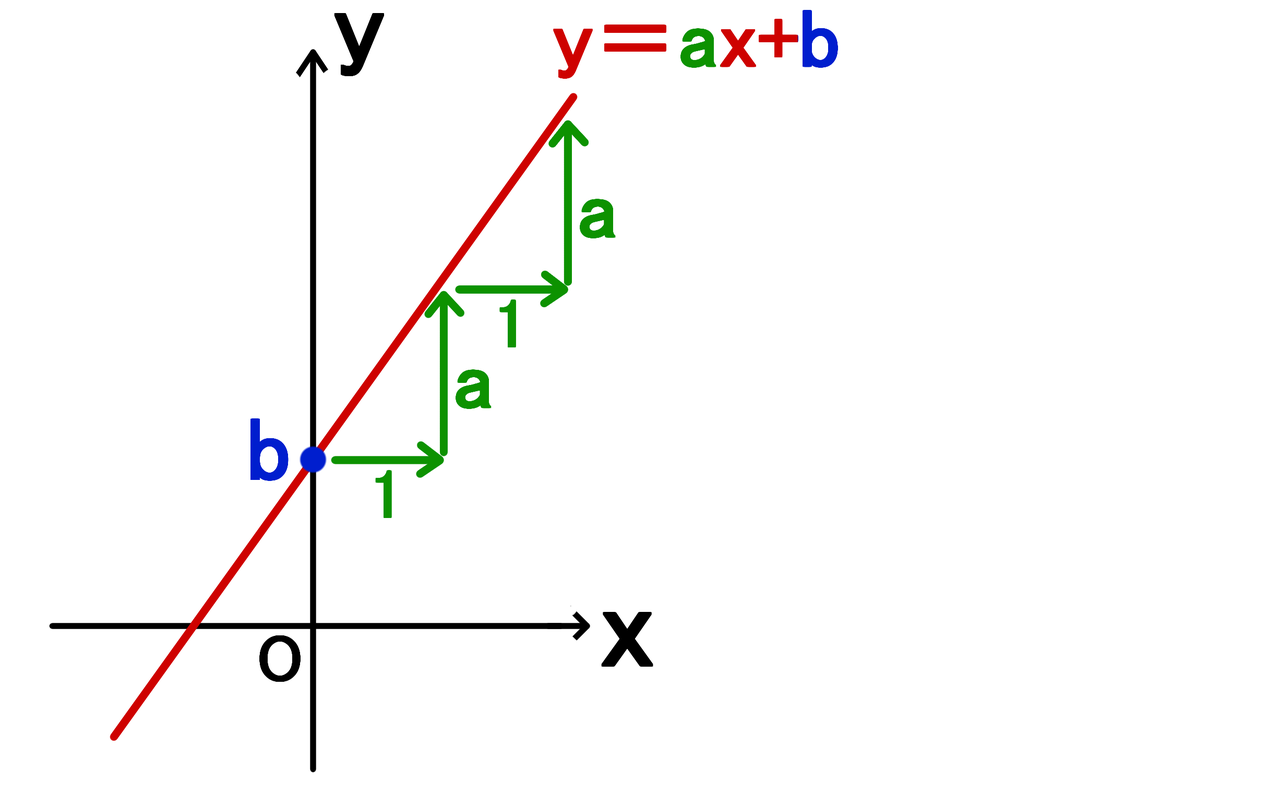
Y Ax Bのグラフと 切片と傾きの意味 中学数学 By じょばんに マナペディア




中3数学 Y Ax 2のグラフ A 0 映像授業のtry It トライイット
関数 について の変域が のとき の変域が である。 このとき、 の値を求めなさい。 , を に代入する。 今回の記事について分かりにくいところ、もっと丁寧に解説してほしかったところがあれば次の動画内でも解説しているのでご参考ください。 関数y=ax2乗式の作り方はこれでバッチリ! aの値の求め方とは? If playback doesn't begin shortly, try restarting your device最小二乗法は計測データの整理に使われる方法である。 n個のデータ(x 1,y 1),(x 2,y 2), (x n,y n)が得られたとする。 に最もフィットする直線をy=axbとすると、 でa,bが求められる。 以下詳しい解説が書いてあります。 y = ax2 y = a x 2 のグラフを 「放物線」といいました が、 y = ax2 bx c y = a x 2 b x c のグラフも 放物線 と呼びます。 形が同じなので、同じ名前で呼ぶんですね。 「二次関数 y = ax2 bx c y = a x 2 b x c のグラフ」のことを「放物線 y = ax2 bx c y = a x 2 b x c 」と呼びます。 また、 y = ax2 bx c y = a x 2 b x c をこの 放物線の方程式 と呼びます。



中学数学 Y Ax 2 図形との融合問題 中学数学の無料オンライン学習サイトchu Su




Y Ax 2 Bx C のグラフのかき方 事後テスト解答例 Kyokuryo Math




二次関数とグラフ 中3数学 高校数学 Irohabook
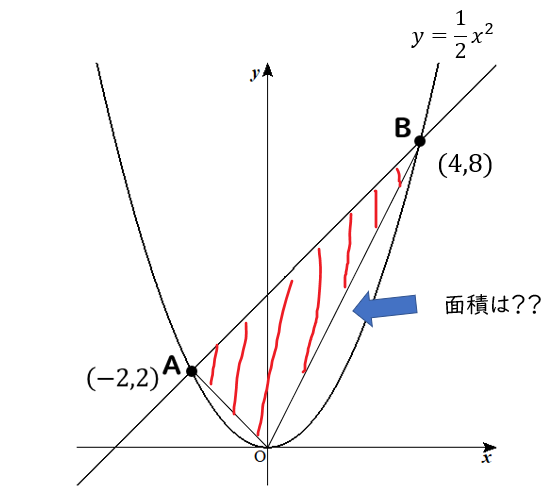



Y Ax2乗の利用 放物線と直線による面積 中学3年の問題をイチから解説 中学数学 理科の学習まとめサイト
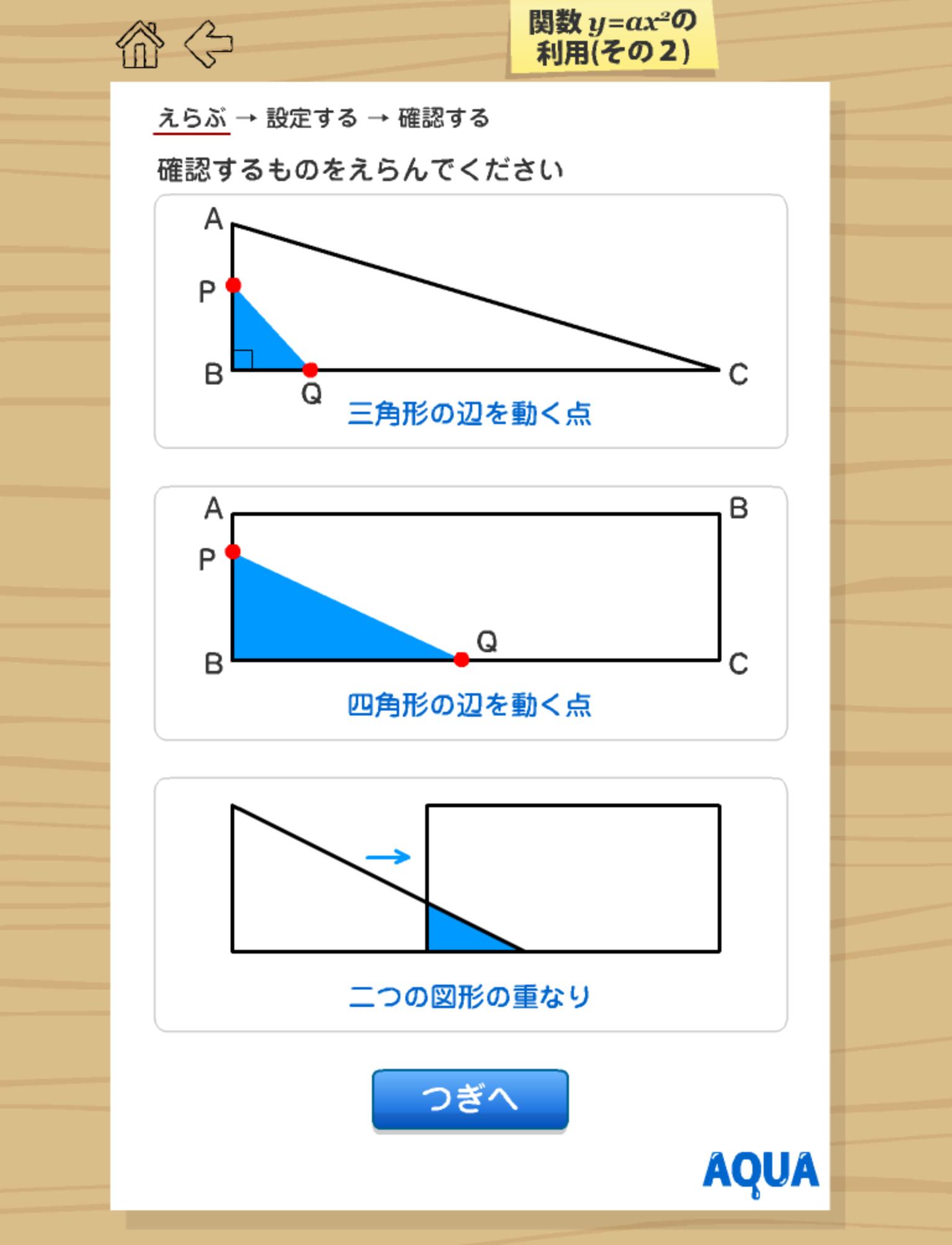



関数y Ax2の利用2 さわってうごく数学 Aquaアクア Fur Android Apk Herunterladen




2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント



中学数学 関数




関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは 数スタ



図のように関数y Ax二乗 二次関数 のグラフ上に2点a Bがそれぞれの座標 Yahoo 知恵袋



ベストyx2乗1 グラフ 最高のぬりえ




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



Y Ax 2



二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師



1




人気ダウンロード 関数yax2乗 グラフの利用 ニスヌーピー 壁紙



1




Y Ax2乗 Aの求め方についてパターン別に解説 発展問題もアリ 中学数学 理科の学習まとめサイト




Y Ax 2 Cのグラフ 数学i フリー教材開発コミュニティ Ftext




例題で学ぶ高校数学 Y Ax2 Q




例題で学ぶ高校数学 Y Ax2




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット




関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ




数学 中3 35 二次関数のグラフ Youtube




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext



数学3年 2次関数 Y Ax2 2次関数のグラフ 2次関数の変域 2次関数の応用 2次関数のグラフ Xの2乗に比例する関数 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3 問題4 正解4 解説




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



2次関数のグラフ Y A X 2 P Q



右の曲線は 関数y Ax二乗のグラフである Aの値と 点aのy座標を Yahoo 知恵袋




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月



Y Ax 2



1




2次関数のグラフと直線



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf



例題で学ぶ高校数学 Y Ax2 Q




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ



授業実践記録



関数y Ax2乗 式の作り方はこれでバッチリ Aの値の求め方とは Youtube



中学数学 関数




基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート



関数y Ax2のグラフ まなびの学園




Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext




中学数学 Y Ax 2 のグラフを読み取る 中学数学の無料オンライン学習サイトchu Su



数学3年 2次関数 Y Ax2 2次関数のグラフ 2次関数の変域 2次関数の応用 2次関数のグラフ Xの2乗に比例する関数 問題1 正解1 解説1 問題2 正解2 解説2 問題3 正解3 解説3 問題4 正解4 解説



二次関数のグラフの書き方



授業実践記録




Y Ax 2の変域 チーム エン




関数y Ax2乗 変域の求め方 変域から式を求める問題を解説 Youtube



2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター




中学校数学 3年生 数量 2乗に比例する関数 Wikibooks



Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf



人気ダウンロード 関数yax2乗 グラフの利用 ニスヌーピー 壁紙




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく




高校数学 Y Ax 2 Qのグラフ1 練習編 映像授業のtry It トライイット




二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ




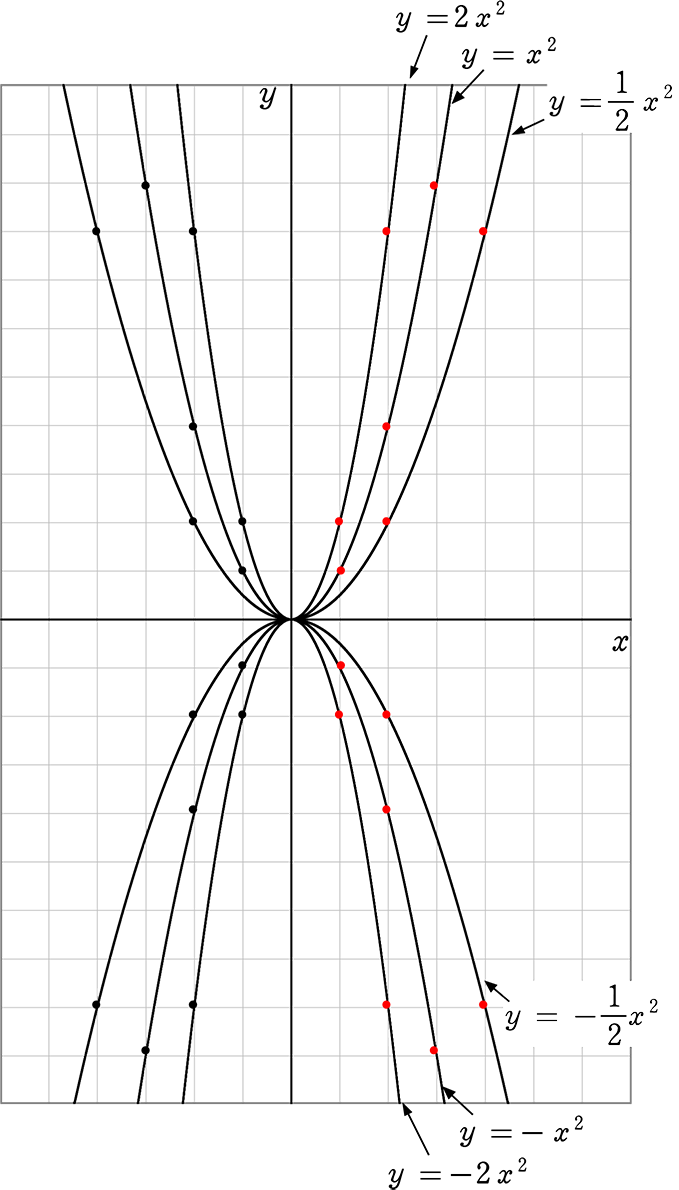
4乗のグラフ 2乗のグラフは学校で習いました 4乗のグラフはどんな 数学 教えて Goo



関数y Ax2のグラフ まなびの学園



4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download



二次関数のグラフの書き方



関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学




24 Y Ax2 Lihat Cara Penyelesaian Di Qanda



文字係数2次関数の頂点




高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット




基本 二次関数y A X P 2のグラフ なかけんの数学ノート



2乗に比例するグラフ 中学から数学だいすき




2次関数 変域 変域からの式の決定 基 標 数学の解説と練習問題




基本 二次関数y A X P 2のグラフ なかけんの数学ノート



2次関数のグラフと係数



図の1のように 関数y Ax二乗のグラフ上に X座標が4 Y座 Yahoo 知恵袋




中学数学 二次関数y Ax2のグラフから式を3秒で読み取る方法 Qikeru 学びを楽しくわかりやすく
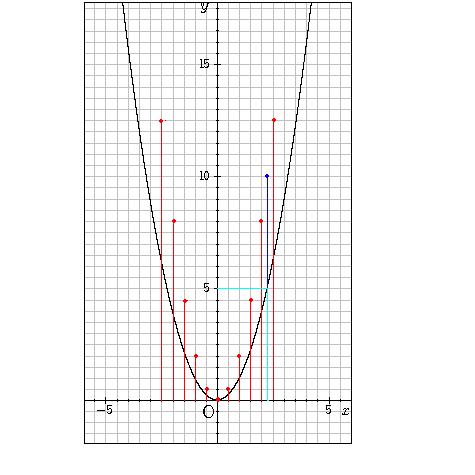



Y 2x 2のグラフ Takapの数学日記




中3 関数 Y Ax2 まとめ 中学生 数学のノート Clear



2乗に比例する関数 グラフ



ねらい 関数y ax2のグラフをかき その特徴を理解する Ppt Download




中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



数学i 2次関数 2 2 Y Ax 2 Qのグラフ Youtube




中3 数学 y Xの二乗の値の変化 中学生 数学のノート Clear



2乗に比例するグラフ 中学から数学だいすき




Aは関数y Ax二乗のグラフと直線y 3分の2x 4との交点 Bは直線y 3分の2x Clear



2乗に比例する関数 グラフ




2次関数 Y Ax Qのグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア




2次関数のグラフ




中3 Y Ax二乗のグラフの性質 変域の求め方 中学生 数学のノート Clear




例題で学ぶ高校数学 Y Ax2



高校数学 指数関数y A Xのグラフ 受験の月



二次関数のグラフと解の存在範囲の問題をわかりやすく解説



1
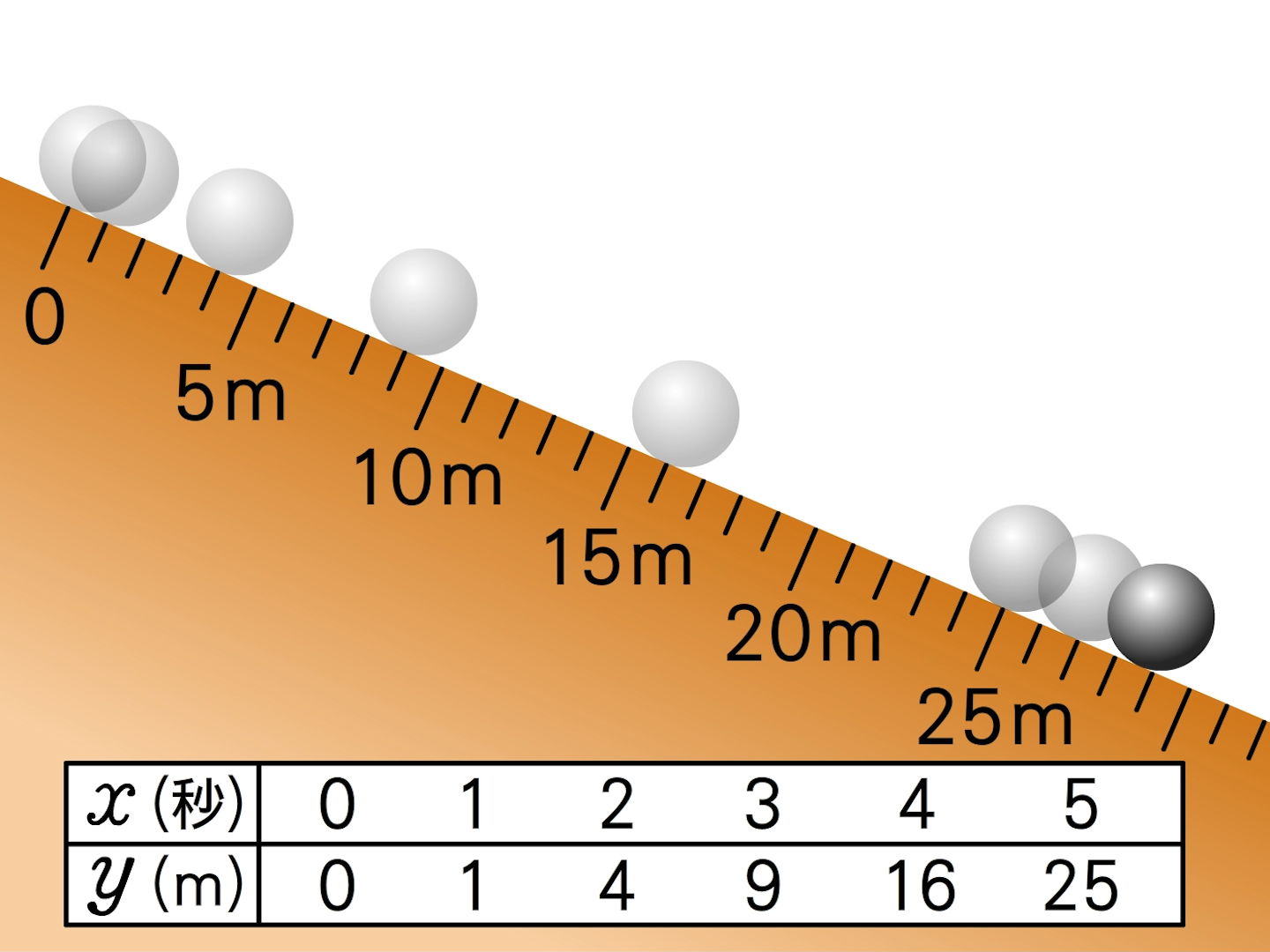



3年 関数 Y Ax 数学イメージ動画集 大日本図書




4 関数 Y Ax 2 1章 関数とグラフ 3 関数 Y Ax 2 の値の変化 5時間 Ppt Download



関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ



0 件のコメント:
コメントを投稿