500 write the equation for a center of (2,4) what is x^2 4x y^2 8y = 2?When p is positive, the parabola opens upward When p is negative, the parabola opens downward (x h)2 = 4p(y k) The Standard Form of the Equation with Vertex (h, k) For a parabola with an axis of symmetry parallel to the xaxis and a vertex at (h, k), the standard form is The equation of the axis of symmetry is y = k For a horizontal parabola, focus = (hp,k) ∴ (hp,k) = (3,2) ⇒hp = 3 and k= 2 For a horizontal parabola the equation of directrix is x = h−p ∴ h−p =−1 Solving the equations hp =3 and h−p = −1, we get h = 1 and p = 2 ∴ vertex =(1,2) equation of parabola(y−k)2 = 4p(x−h) ⇒(y−2)2 = 8(x−1)2
Pslv Conic Section
If the focus of the parabola (y-k)^2=4(x-h)
If the focus of the parabola (y-k)^2=4(x-h)-$$ Parabola (xh)^2=4p(yk) $$ $$ Vertex (h, k) , Focus (h, kp) $$ h k p Add Parabola Ellipse $$ Ellipse (xh)^2/a^2(yk)^2/b^2=1 $$ Center (h, k) Length of major axis is 2a Length of minor axis is 2b h k a b Add Ellipse HyperbolaLearn termparabolas = (x h)^2=4p(y k) (y k)^2=4p(x h) with free interactive flashcards Choose from 63 different sets of termparabolas = (x h)^2=4p(y k) (y k)^2=4p(x h) flashcards on Quizlet




What Are The Formula Of Parabola Brainly Ph
In algebra, dealing with parabolas usually means graphing quadratics or finding the max/min points (that is, the vertices) of parabolas for quadratic word problemsIn the context of conics, however, there are some additional considerations To form a parabola according to ancient Greek definitions, you would start with a line and a point off to one side100 the circle equation what is (xh)^2(yk)^2=r^2?Algebra Conic sections ellipse, parabola, hyperbola Section Solvers Solvers Lessons Lessons Answers archive Answers Click here to see ALL problems on Quadraticrelationsandconicsections;
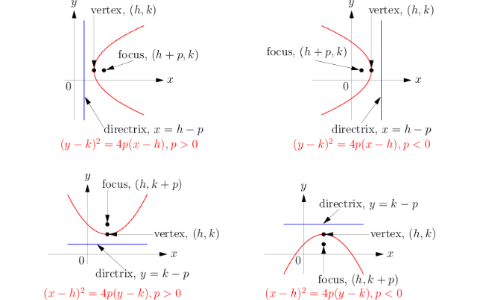
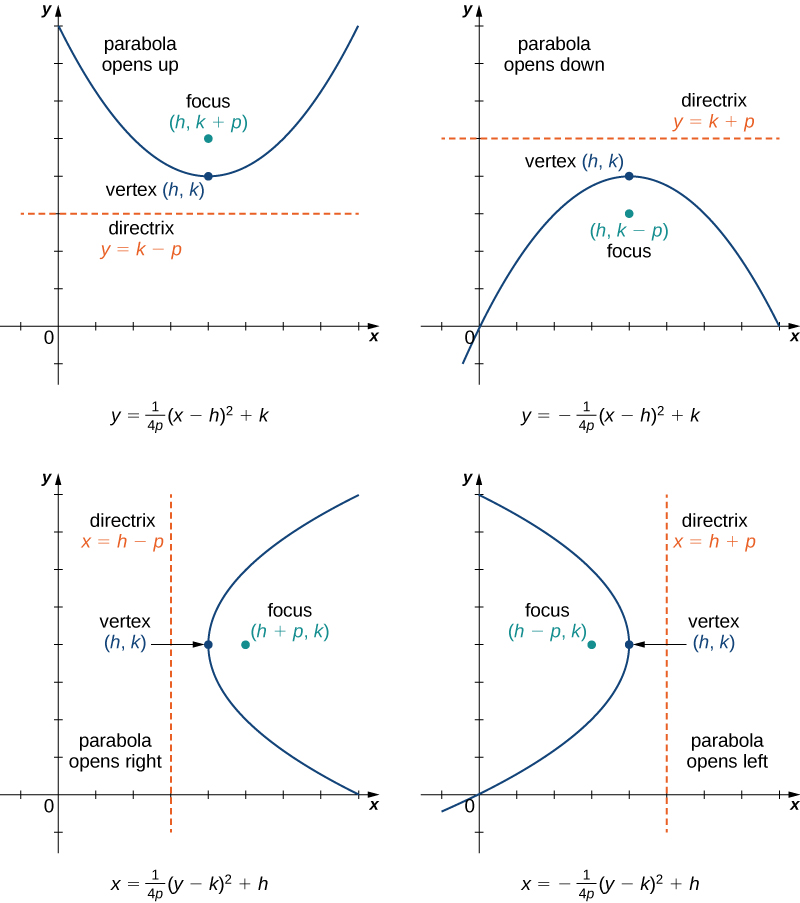
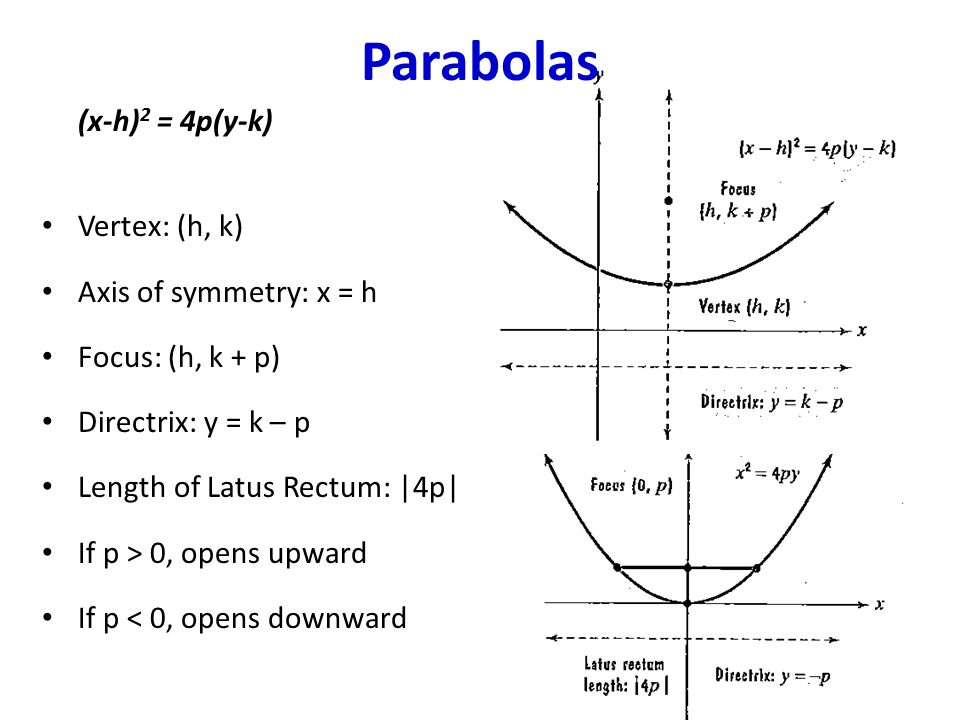
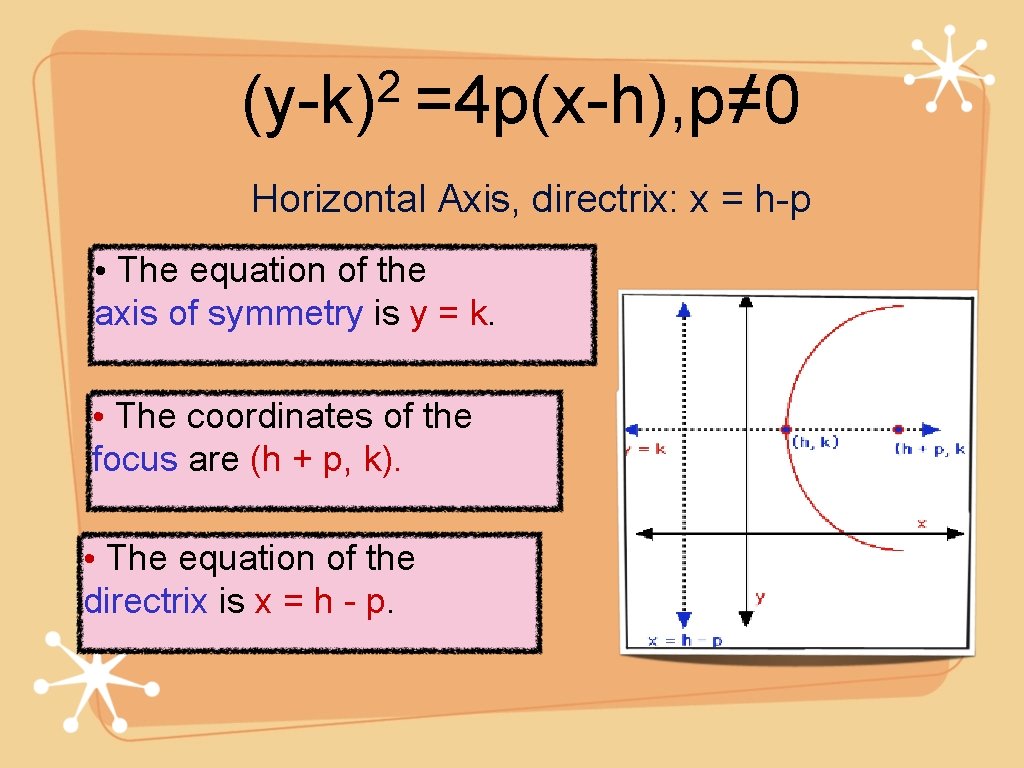
The standard form is (x – h)2 = 4p (y – k), where the focus is (h, k p) and the directrix is y = k – p If the parabola is rotated so that its vertex is (h,k) and its axis of symmetry is parallel to the xaxis, it has an equation of (y – k)2 = 4p (x – h), where the focus is (h p, k) and the directrix is x = h – pThe focus is located at (h, k p) In this example the focus is at (4, 3) so k p = 3 But k = 6 so p = 3 6 = 3;\({\text{Parabolas (Alternative Vertex Form)}}\) \({\text{Equation Vertex Form}}\) \((xh)^2=4p(yk)\) \((yk)^2=4p(xh)\) \({\text{Focus}}\) \((h,kp)\)
In order to solve problems in which the vertex (h, k) of a parabola is not at the origin, one of the following standard forms should be used, depending on the axis (vertical or horizontal) the original equation indicates 1) Symmetry of x = h (vertical) (x – h)2 = 4p(y – k) The focus will be (h, k p) The directrix will be y = k – p 2)0 find the focus of the parabola x^2=22y what is (0,11/2)? Example 93 2 Put the equation of the parabola y = 8 ( x − 1) 2 2 in standard conic form Find the vertex, focus, and axis of symmetry Solution From your earlier work with quadratics, you may already be able to identify the vertex as (1,2), but we'll go ahead and put the parabola in the standard conic form




Solved For The Equation Of The Parabola Given In The Form Chegg Com



Parabola By Monica Gil On Prezi Next
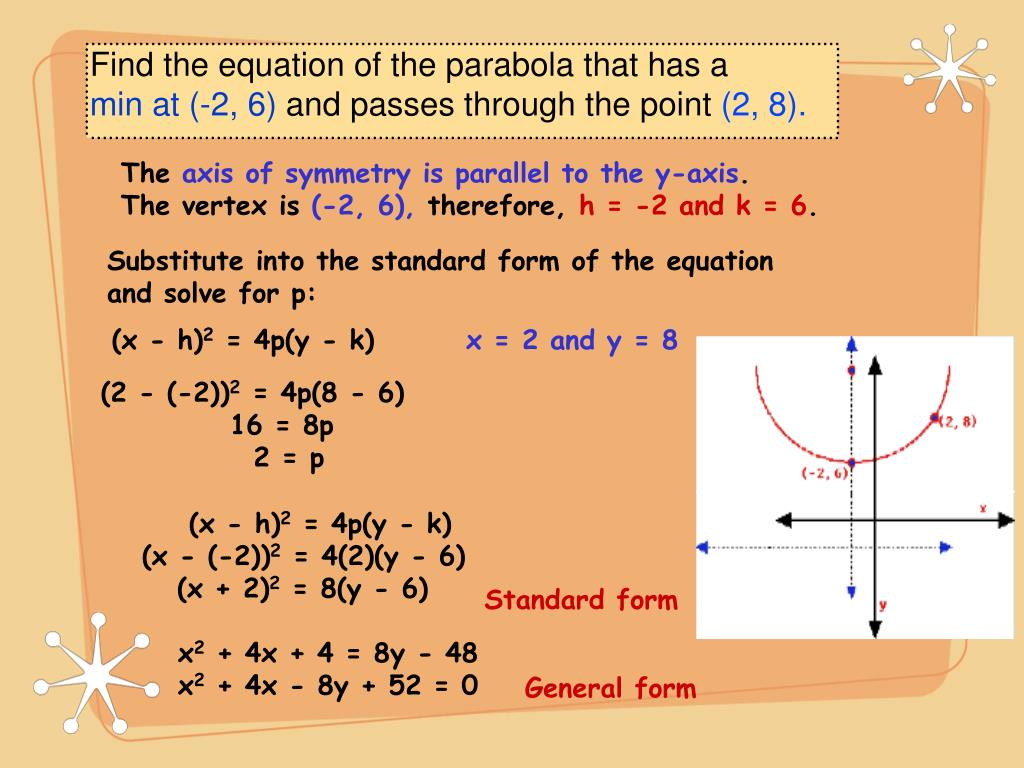
Vertex is on line Y = 2 so, Y coordinate of vertex is 2 Latus rectum is 6, so 4p = 6 Vertex on Y = 2 and passes through (2,8), so parabola is vertical and opens upwards Standard equation for this parabola is (X h)^2 = 4p(Y k) We kn The equation of the parabola in focus vertex form is (x h) 2 = 4p(y k) The vertex is at (h,k) giving us h = 4, k = 6;Each parabola is, in some form, a graph of a seconddegree function and has many properties that are worthy of examination Let's begin by looking at the standard form for the equation of a parabola The standard form is (x h) 2 = 4p (y k), where the focus is (h, k p) and




Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation



Conic Sections Calculus Volume 2
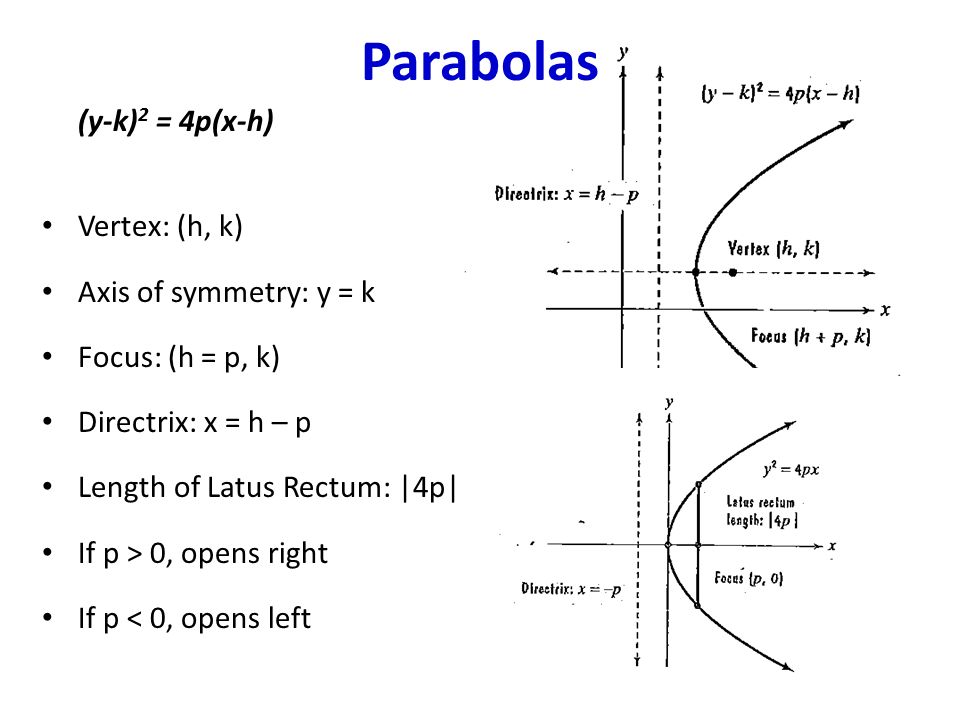
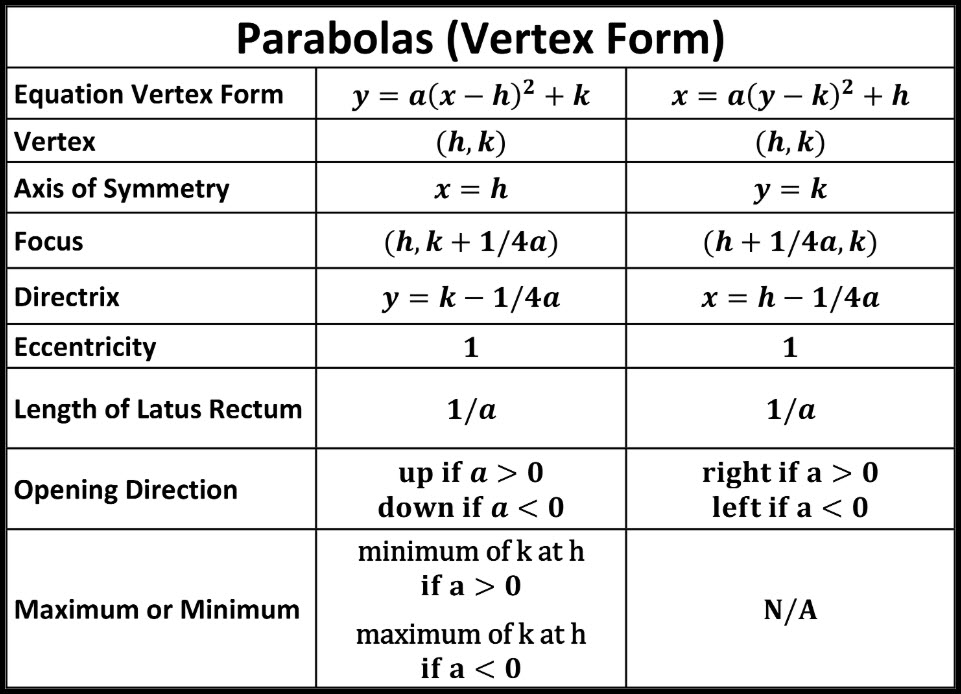
2 PARABOLA with vertex at (0,0) y2 4px Opens left or right x2 4py Opens up or down 3 PARABOLA (y k) 2 4p (x h) Opens left or rightStart studying Parabola (xh)^2=4p(yk) Learn vocabulary, terms, and more with flashcards, games, and other study toolsConic Sections Formulas Parabola Vertical Axis Horizontal axis equation (xh)2=4p(yk) (yk)2=4p(xh) Axis of symmetry x=h y=k Vertex (h,k) (h,k) Focus (h,kp) (hp,k) Directrix y=kp x=hp Direction of opening p>0 then up;



Ppt Parabola Powerpoint Presentation Free Download Id



More Conic Sections Objective Given A Translation I Can Graph An Equation For A Conic Section Ppt Download
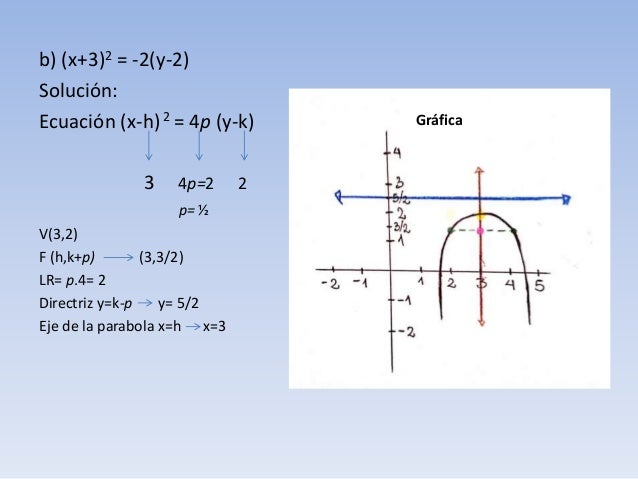
PARABOLA CON VERTICE FUERA DEL ORIGEN Teorema 2 PARABOLA HORIZONTAL PARABOLA VERTICAL (y – k)2 = 4p (x –h) (x –h)2= 4p (y – k) V (h,k) V (h,k) F (h p, k) F (h k, p) Directriz x = h p Directriz y = k pLongitud del lado recto 4P Longitud del lado recto 4P P> 0 abre a la derecha P> 0 abre hacia arriba P< 0 abre a la izquierda P< 0 1 Answer1 You are right since the vertex is above the focus, the parabola must open downwards So p = − 10 and the parabola has equation ( x − 1) 2 = − 40 ( y − 2) Note that the right hand side is never negative because for all points on the parabola y ≤ 2 (because the parabola opens downwards) For parabolas that open either up or down, the standard form equation is (x h)^2 = 4p(y k) For parabolas that open sideways, the standard form equation is (y k)^2 = 4p(x h) The vertex or tip of our parabola is given by the point (h, k)
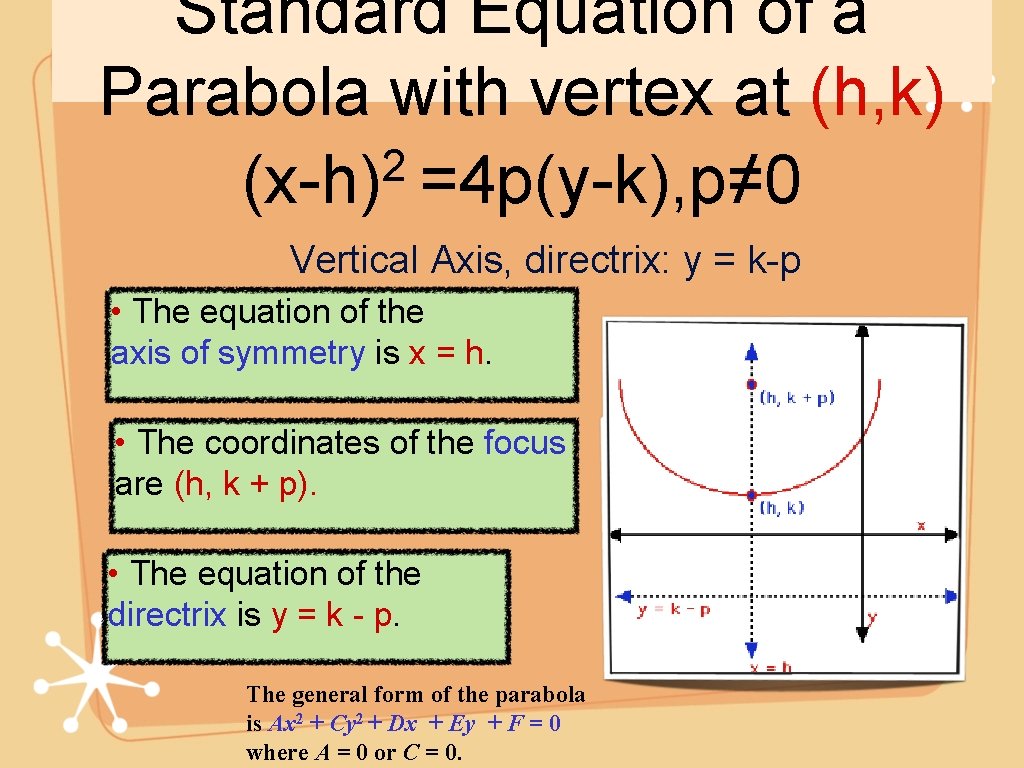



Parabola Conic Section Warmup Graph The Following Parabola



Pslv Conic Section
The standard form is (x h) 2 = 4p (y k), where the focus is (h, k p) and the directrix is y = k p If the parabola is rotated so that its vertex is (h,k) and its axis of symmetry is parallel to the xaxis, it has an equation of (y k) 2 = 4p (x h), where the focus is (h p, k) and the directrix is x = h p How do you write the Key Concepts A parabola is the set of all points (x, y) in a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrix The standard form of a parabola with vertex (0, 0) and the x axis as its axis of symmetry can be used to graph the parabolaThen graph the parabola The equation is in standard form and the squared term is x, which means that the parabola opens vertically Because 4p = 12, p = 3 and the graph opens upward The equation is in the form (x — h)2 = 4p (y — k) , so h = 3 and k = —4 Use the values of h, k, and p to determine the characteristics of the parabola




10 6 Graphing And Classifying Conicsd And Classifying Conics Writing And Graphing Equations Of Conics Parabolas Circles Ellipses Because The Parabola Opens To The Left It Has Pdf Document




Ppt 8 2 Graph And Write Equations Of Parabolas Powerpoint Presentation Id
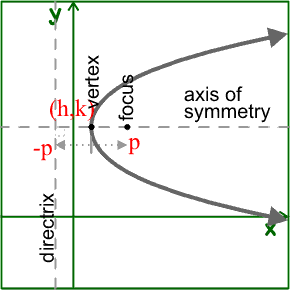
702 Parabolas This is an original lesson based on OpenStax Precalculus lesson 103 Find the focus, vertex, and directrix of a parabola Write the standard equation of a parabola Graph a parabola The L'Umbracle sculpture garden is covered with arches shaped like parabolas that open down Of all arch types, parabolic arches have the mostPlug the values into the equation (x h) 2 = 4p(y k) so (x 4) 2 = 4(3)(y 6) Simplify giving (x 4PARABOLA Definition A parabola is the collection of all points in the plane that are the same distance from a fixed point, called the focus (F), as they are from a fixed line, called the directrix (D) Standard Form (x h) 2 = 4p(y k) (y k) 2 = 4p(x h) p > 0 Parabola opens UP p > 0 Parabola opens RIGHT p < 0 Parabola opens DOWN p < 0
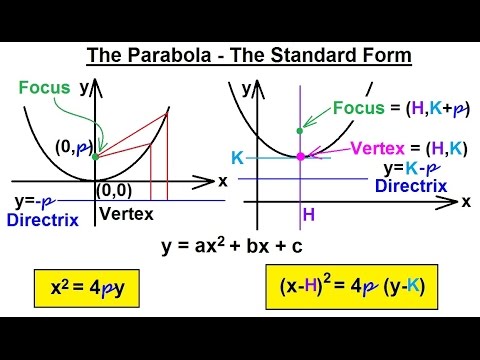



Precalculus Algebra Review Conic Sections 5 Of 27 The Parabola Standard Form Youtube



Www Kentschools Net Wp Content Blogs Dir 130 Files 17 04 9 1 New Pdf
The standard form is (x h) 2 = 4p (y k), where the focus is (h, k p) and the directrix is y = k p If the parabola is rotated so that its vertex is (h,k) and its axis of symmetry is parallel to the xaxis, it has an equation of (y k) 2 = 4p (x h), where the focus is (h p, k) and the directrix is x = h pLatex{\left(xh\right)}^{2}=4p\left(yk\right)/latex Key Concepts A parabola is the set of all pointslatex\,\left(x,y\right)\,/latexin a plane that are the same distance from a fixed line, called the directrix, and a fixed point (the focus) not on the directrixNote • (x h)2 = 4p (y k) Parabola open up (U) if p>0 and opend down (D) if p0 and opend to the left (L) if p
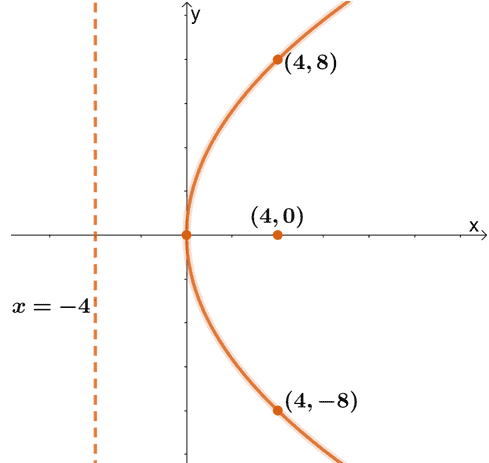



Parabola Properties Components And Graph



Pslv Conic Section
Similarly, if we are given an equation of the form y 2 AyBxC=0, we complete the square on the y terms and rewrite in the form (yk) 2 =4p(xh) From this, we should be able to recognize the coordinates of the vertex and the focus as well as the equation of the directrixBoth points of xintercept satisfy the given equation y = (x h)^2 k, therefore (1,0) 0 = (1 h)^2 k —> k h^2 2h 1 = 0 (1) (8,0) 0 = (8 h)^2The Parabola Algebraic Definition of The Parabola Recall that the standard equation of the parabola is given by y = a (x h) 2 k If we are given the equation of a parabola y = ax 2 bx c we can complete the square to get the parabola in standard form Geometry of the Parabola We can define a parabola as follows
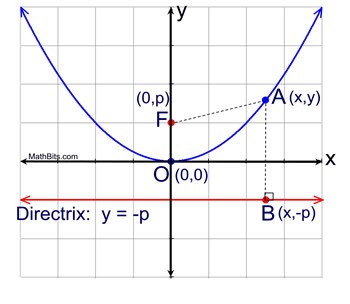



Parabola Equations Mathbitsnotebook Geo Ccss Math




Focus Directrix Of A Parabola From Equation Video Khan Academy
Parabola – Properties, Components, and Graph Parabolas are the first conic that we'll be introduced to within our Algebra classes These conics that open upward or downward represent quadratic functionsThis is also what makes parabolas special – their equations only contain one squared termGiven {eq}(x h)^2 = 4p(y k), {/eq} the ordered pairs representing the vertex and focus are _____ and _____, respectively The directrix is the line defined by the The standard form is (x h) 2 = 4p (y k), where the focus is (h, k p) and the directrix is y = k p If the parabola is rotated so that its vertex is (h,k) and its axis of symmetry is parallel to the xaxis, it has an equation of (y k) 2 = 4p (x h), where the focus is (h p, k) and the directrix is x = h p




Math Test Conic Sections Flashcards Quizlet



Section 10 5 Parabolas
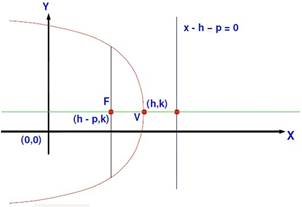
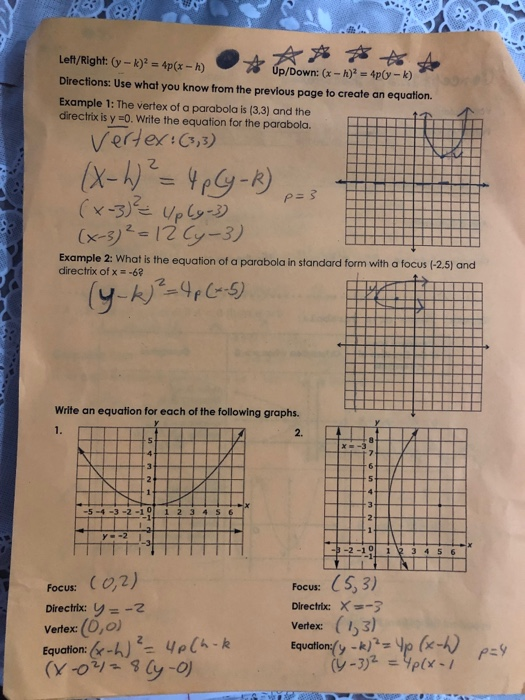
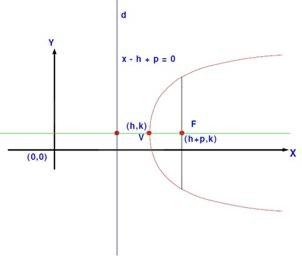
If a parabola has a horizontal axis, the standard form of the equation of the parabola is this (y k)2 = 4p(x h), where p≠ 0 The vertex of this parabola is at (h, k) The focus is at (h p, k) The directrix is the line x = h p The axis is the line y = k If p > 0, the parabola opens to the right, and if p < 0, the parabola opens toLearn how to graph a parabola in the form y=(xh)^2k!Make sure to like this video if you found it helpful and feel free to leave feedback in the comments se For parabolas that open sideways, the standard form equation is (y k)^2 = 4p(x h) The vertex or tip of our parabola is given by the point (h, k) For parabolas that open up and down, the focus point is given by (h, k p) For parabolas that




X H 2 4p Y K Y K 2 4p X H If The X Value Is Greater Than 1 The Parabola Will Open Up If The X Value Is Less Than 1 The Parabola Will Open Ppt Download




Como Pasar De La Ecuacion General A La Ecuacion Canonica En La Parabola Youtube
The equation 4a(yk)=(xh) 2 generates a parabola which opens upward if a>0 and opens downward if aQuestion Please explain why the graph of (xh)^2 = 4p(yk) has a yintercept of (xh)^2 = 4p(yk) (0h)^2 = 4p(yk) h^2 = 4p(yk)For this kind of parabola, the attention is centered at the point (h, k p) and the directrix is a lineup located at y = k p On the flip side, the equation of a parabola calculator with a vertex at (h, k) and a horizontal axis of symmetry is described as (y k)^2 = 4p(x h)
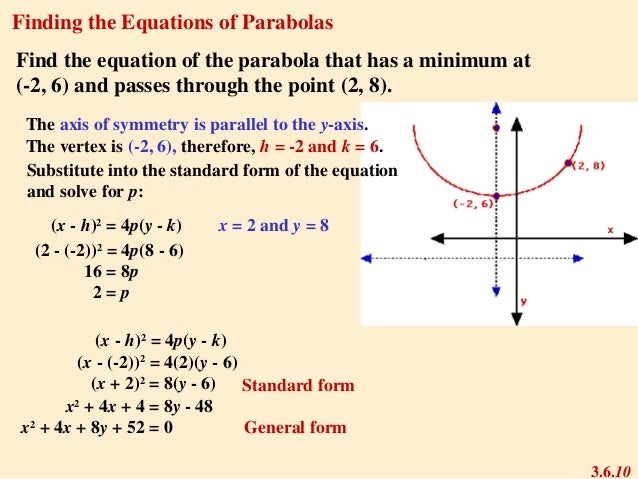



1576 Parabola



To Graph A Parabola We Need To Know The Coordinates Of Its Vertex Focus And The Equation Of Its Axis
The standard form of the equation of a parabola with a vertical axis of symmetry can be written as (x h) 2 = 4p (y k), where (h, k) is the vertex, (h, k p) is the focus, x = h is the axis of symmetry, and y = k – p is the directrix Note that the parabola opens upward if{eq}(yk)^2=4p(xh) {/eq}, then the parabola has a vertical axis The equation can be rewritten as {eq}\dfrac{1}{4p}(yk)^2=(xh) {/eq} If p is negative, the parabola opens leftward, and if p• Given the focus and directrix of a parabola, or the focus and vertex, or the vertex and directrix, write down its equation in the form (xh)2 = 4p(yk) or (yk)2 = 4p(xh) • Graph a parabola given in the form (x h)2 = 4p(y k) or (y k)2 = 4p(x h) and locate its focus, directrix, and axis of symmetry




Lesson 5 1 Parabolas Chart Parabolas With Vertex H K Vertical H K Horizontal H K X H 2 4p Y K Y K 2 4p X H 1 X H 2 4 Opens Upward If P 0 P Course Hero



Solution Find An Equation In Standard Form Of The Parabola Described Vertex At 2 4 Passes Through 0 4 Form Y K 2 4p X H
4 Parabola Definition locus of points in a plane which are equidistant from a given point (the focus) and a given line (the directrix) Parabola (y k)2 = 4p(x h)Title Parabolas 1 Section 102 Parabolas;For the equation of the parabola given in the form (y k)2 = 4p(xh), (a) Identify the vertex, value of p, focus, and focal diameter of the parabola (b) Identify the endpoints of the latus rectum (c) Graph the parabola (d) Write equations for the directrix and axis of symmetry Express numbers in exact, simplest form (y4)² = 16(x4)



1




Equation Of Parabola Directrix Focus Axis Problems With Solutions
The standard form that applies to the given equation is latex{\left(xh\right)}^{2}=4p\left(yk\right)/latex Thus, the axis of symmetry is parallel to the y axis To express the equation of the parabola in this form, we begin by isolating the terms that contain the variable latexx/latex in order to complete the squareDetermine an equation of the parabola with its axis parallel to the y axis and which passes through the three points (0, 1), (1, 0), ( 2, 1) Hence find the vertex, focus, directrix and sketch the graph Solution Since the axis of symmtry is vertical, the equation of parabola is of the form (x−h)2 =This is a topic level video of Graphing a Parabola of the Form y = a(xh)^2 k for the ASU College Algebra and Problem Solving CourseJoin us!https//wwwed
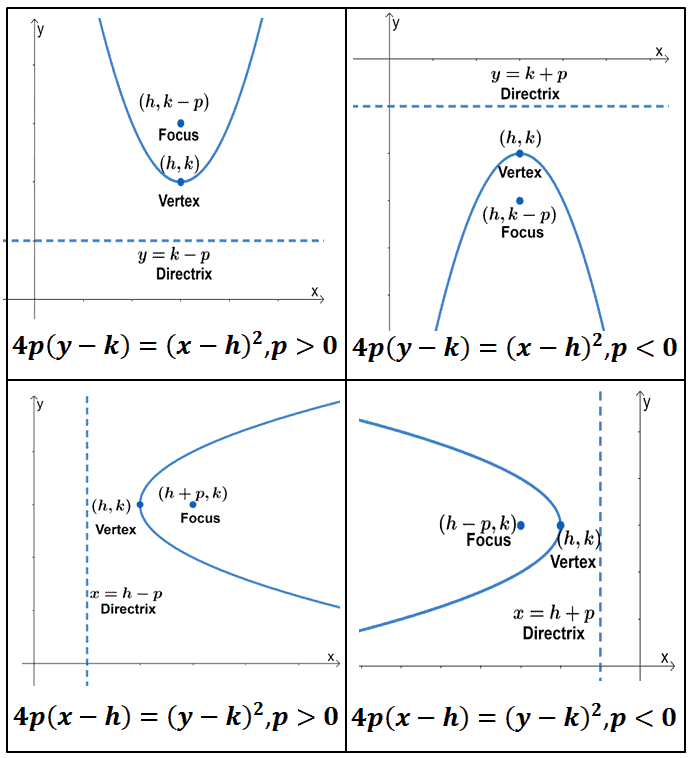



Parabola Properties Components And Graph




Math1 2
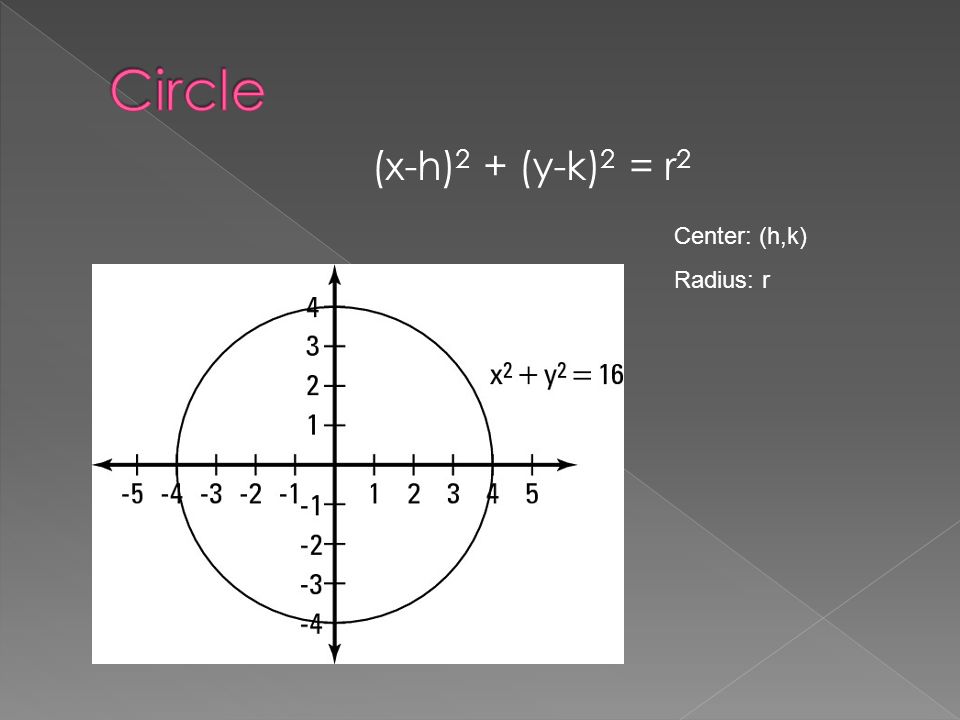
400 Identify which of the two equations is a circle a) (x9)^2 (y2)^2 = 49 b) 25x^2 4y^2 =100 The circle is equation a Because when we divide the 49 out, each fraction will have the same denominator whereas in equation b, when we divide the 100 out, each fraction will have a different denominator
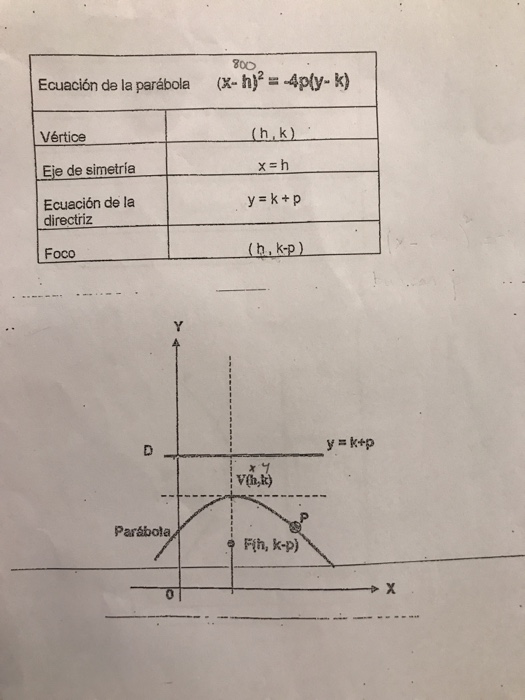



300 Ecuacion De La Parabola X H 2 4p Y K Vertice Chegg Com




Parabolas Parabolas



Parabolas
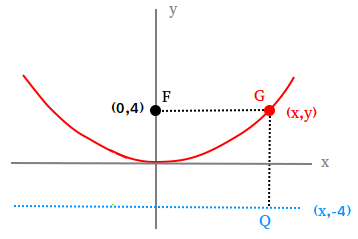



Parabola Definition And Equation



Solution Find The Standard Equation With Focus 2 0 And Directrix X 4 Y K 2 4p X H This Is As Far As I Have Gotten I Think That The Vertex Is 1 0



Parabolas



Chapter 10 Analytic Geometry Section 10 1 Parabolas Flip Ebook Pages 1 9 Anyflip Anyflip



Cochranmath Copy Of Parabola




Shifted And Horizontal Parabolas Precalculus Conic Sections Lesson 3 Youtube
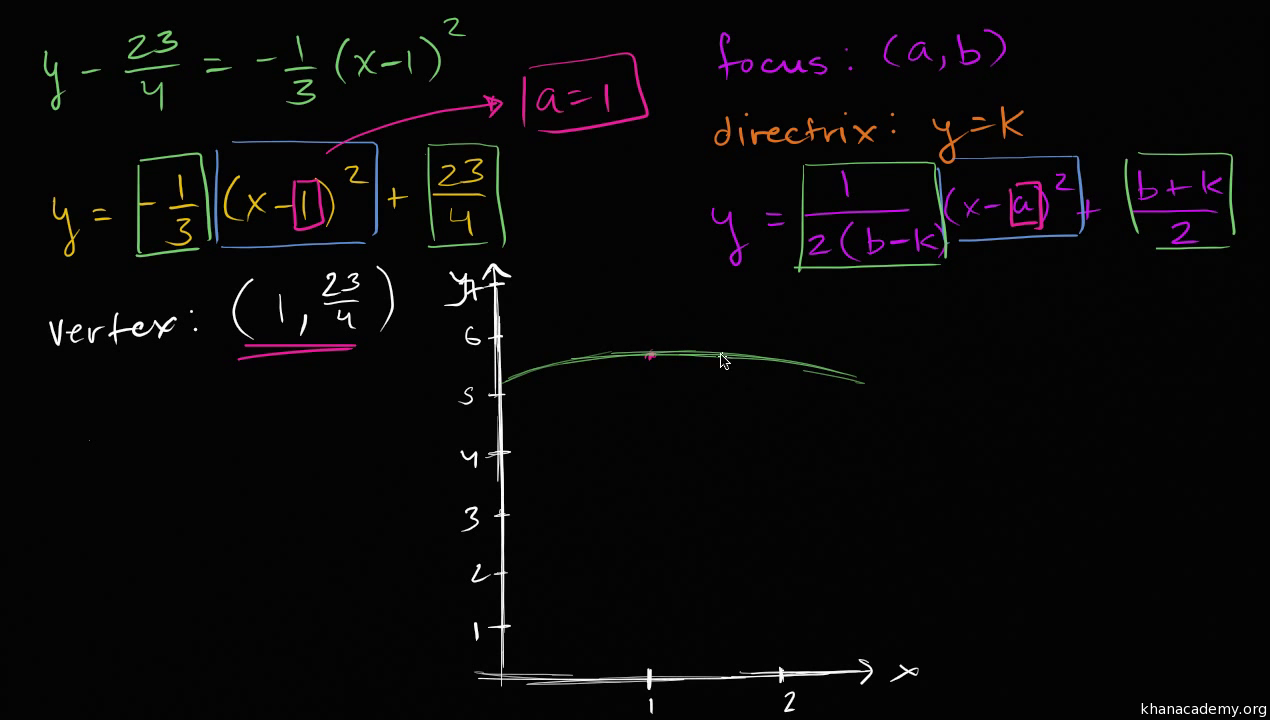



Focus Directrix Of A Parabola From Equation Video Khan Academy




What Are The Formula Of Parabola Brainly Ph




Unit 2 Algebra 2 With Mikhail
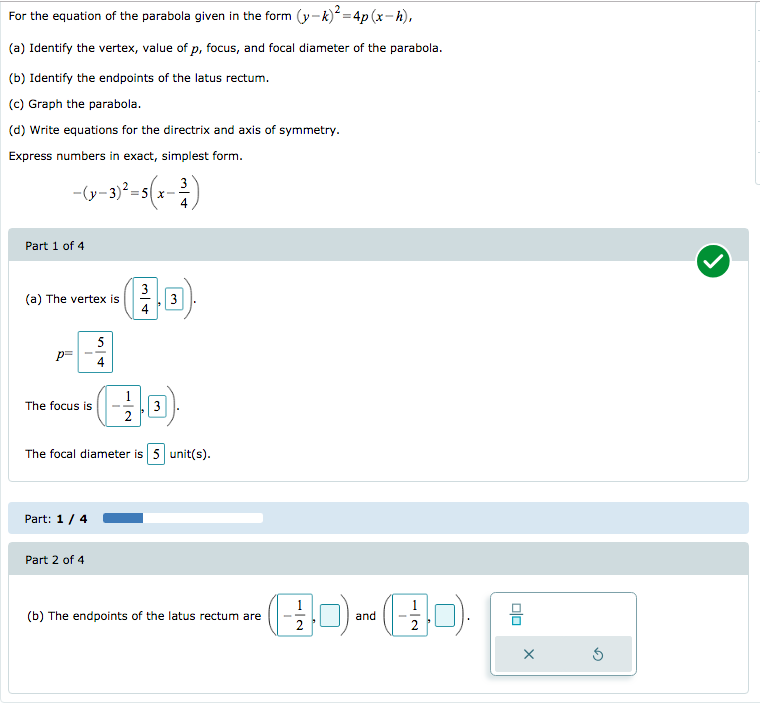



Solved For The Equation Of The Parabola Given In The Form Chegg Com



Lesson 4 Parabolas In This Lesson Students Will Become Familiar With The Equations And Graphs Of Parabolas The Definition Of A Parabola Will Be Learned Both Algebraically And Using The Distance Relationship Students Will Learn How To Construct A Parabola




Precalculus Algebra Review Conic Sections 5 Of 27 The Parabola Standard Form Youtube




Parabolas With Vertex At H K Ck 12 Foundation
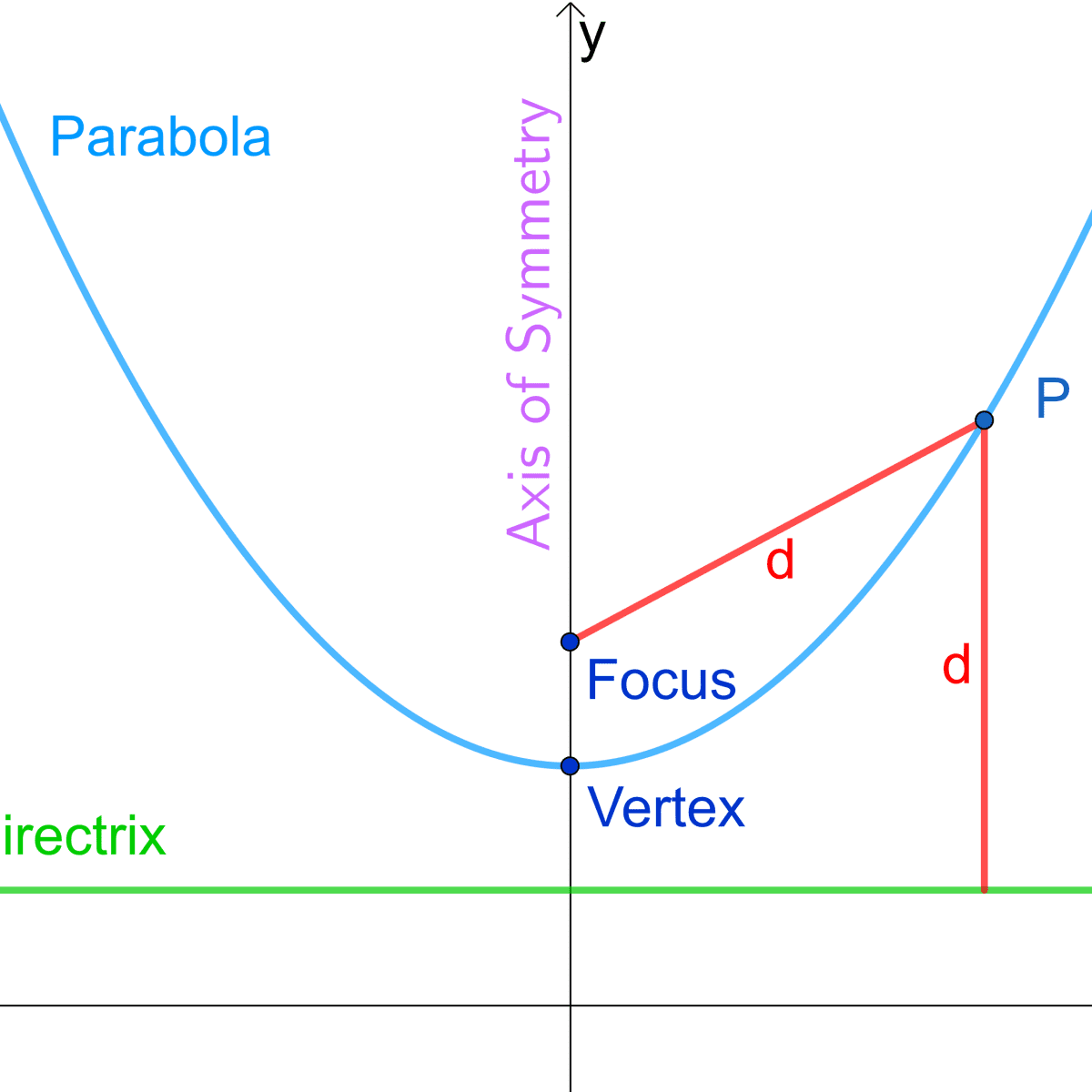



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation



Parabolas Andymath Com



Ecuacion De La Parabola 2




Parabolas Andymath Com




Conic Sections And A New Look At Parabolas Ppt Download



More Conic Sections Objective Given A Translation I Can Graph An Equation For A Conic Section Ppt Download




Conic Sections Formulas Pages 1 1 Flip Pdf Download Fliphtml5



Http Www Lonestar Edu Departments Learningcenter Conicsections Pdf



Left Right Y K 2 4p X H Directions Use What You Chegg Com




Parabola Conic Section Warmup Graph The Following Parabola




Parabola Conic Section Warmup Graph The Following Parabola
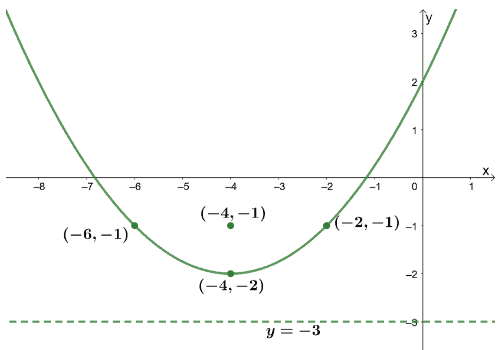



Parabola Properties Components And Graph
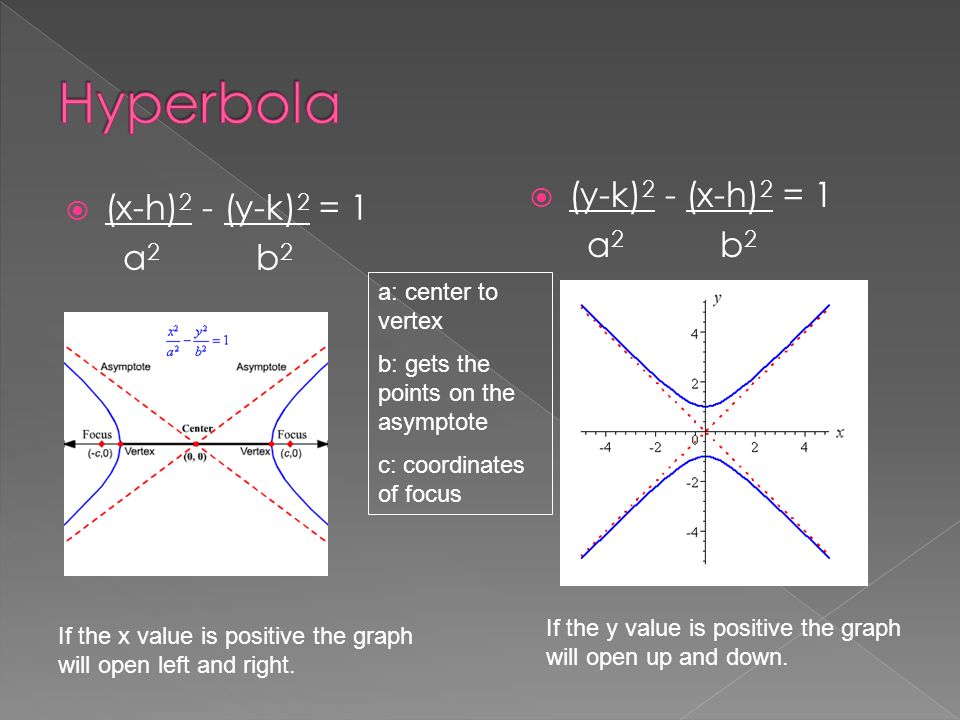



X H 2 4p Y K Y K 2 4p X H If The X Value Is Greater Than 1 The Parabola Will Open Up If The X Value Is Less Than 1 The Parabola Will Open Ppt Download




8 2 Graph And Write Equations Of Parabolas Analytic Geometry Geometry




Parabolas Con Vertice En H K Ck 12 Foundation
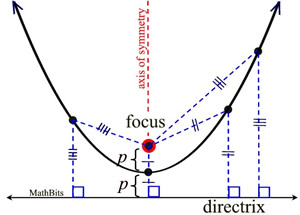



Parabola Equations Mathbitsnotebook Geo Ccss Math




Parabolas
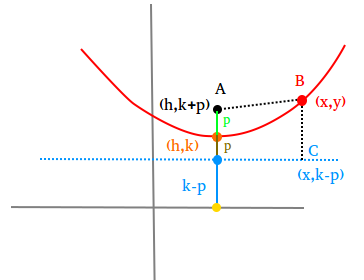



Parabola Definition And Equation




Parabola Transporte En El Peru




Focus Of A Parabola



Http Home Miracosta Edu Dbonds Math 155 lecture notes section 10 1 Pdf




The Young Math Analysis 101 Rwa 1 Unit M Concept 4 6 Conic Sections In Real Life Scenarios




Today In Precalculus Go Over Homework Notes Parabolas With Vertex Other Than 0 0 Homework Ppt Download



Parabola Conic Section Warmup Graph The Following Parabola
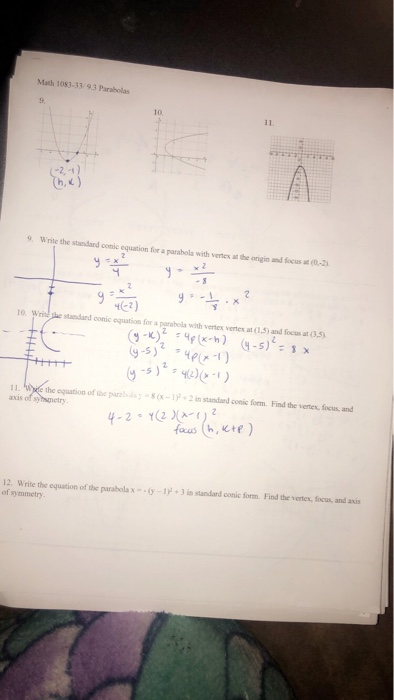



Solved The Directions For 9 11 Is To Write An Equation Fo Chegg Com



Conic Sections Parabolas Summary Analysis Sparknotes



What Is The Equation Of A Parabola With Vertex 3 2 And Focus At 0 2 Quora




Ppt Parabola Powerpoint Presentation Free Download Id



2




Parabolas With Vertex At H K Ck 12 Foundation
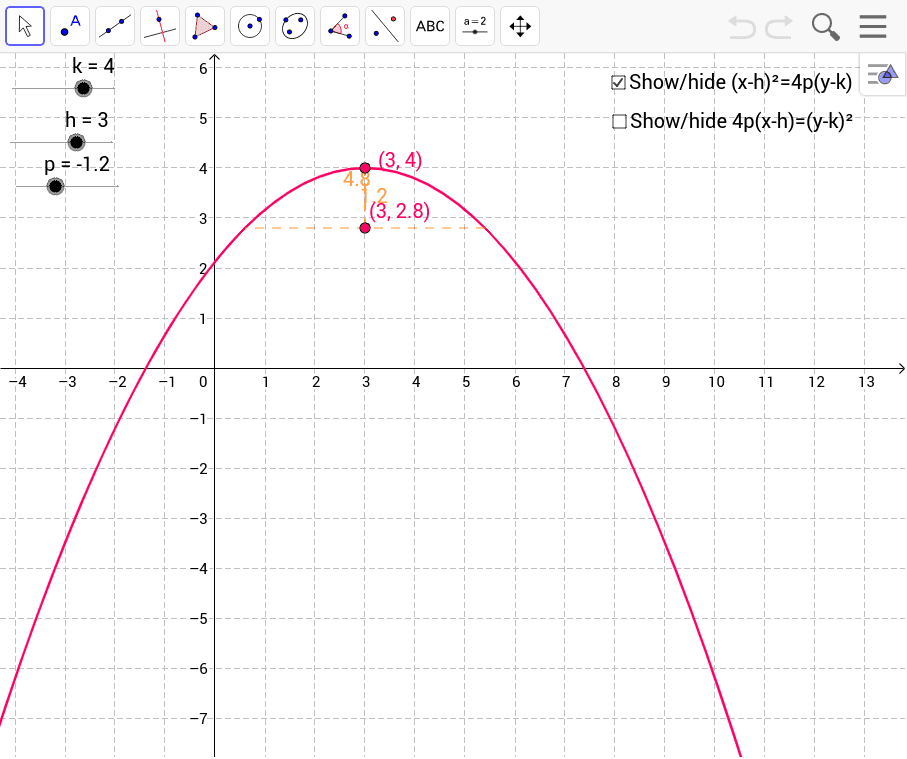



Access Parabola Equation Geogebra



Parabolas




10 2 Introduction To Conics Parabolas Free Download Pdf



1
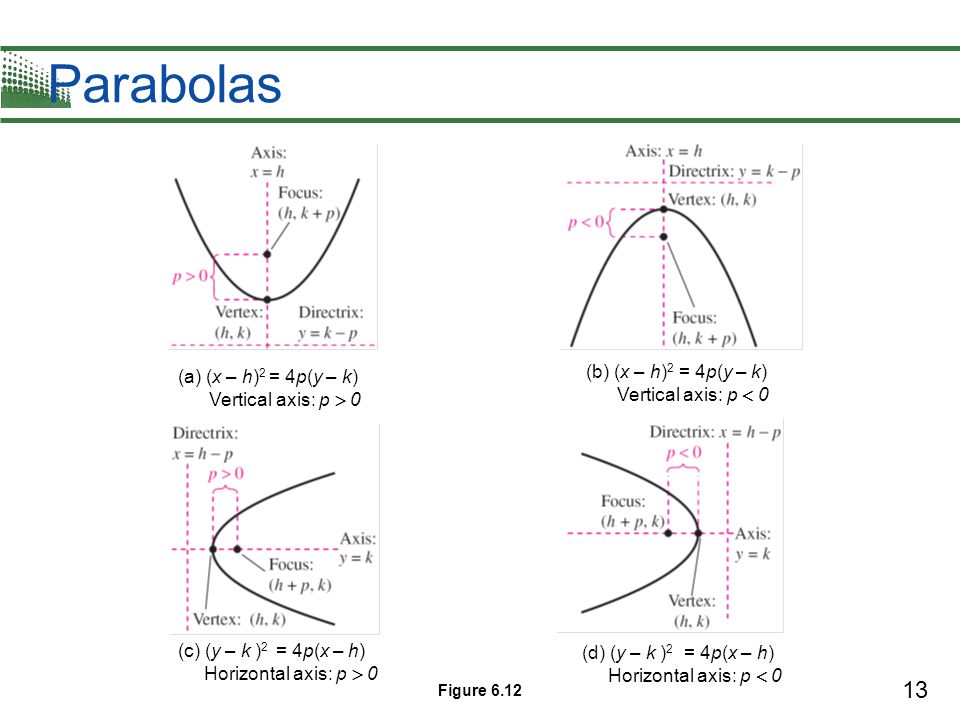



Copyright C Cengage Learning All Rights Reserved Ppt Video Online Download



Http Mrsbrach Weebly Com Uploads 2 3 1 8 10 2notes Pdf



X H 2 4p Y K Y K 2 4p X H If The X Value Is Greater Than 1 The Parabola Will Open Up If The X Value Is Less Than 1 The Parabola Will Open Ppt Download




Parabolas




Parabolas Parabolas



Conicas Ecuaciones Parametricas Y Coordenadas Polares Math



Www Kentschools Net Wp Content Blogs Dir 130 Files 17 04 9 1 New Pdf



Ecuacion De La Parabola 2



1




Parabolas



Every Day I M Calculatin Rwa1 Unit M Concepts 4 6 Conic Sections In Real Life



Http Home Miracosta Edu Dbonds Math 155 lecture notes section 10 1 Pdf




For The Equation Of The Parabola Given In The Form Chegg Com
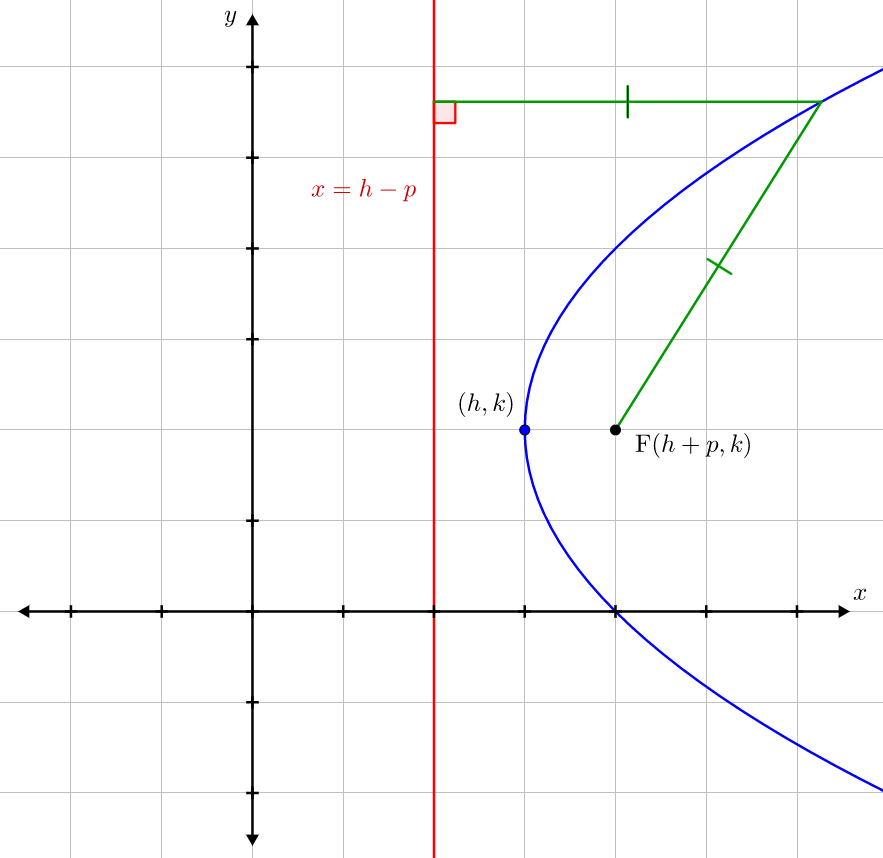



Conic Sections Brilliant Math Science Wiki
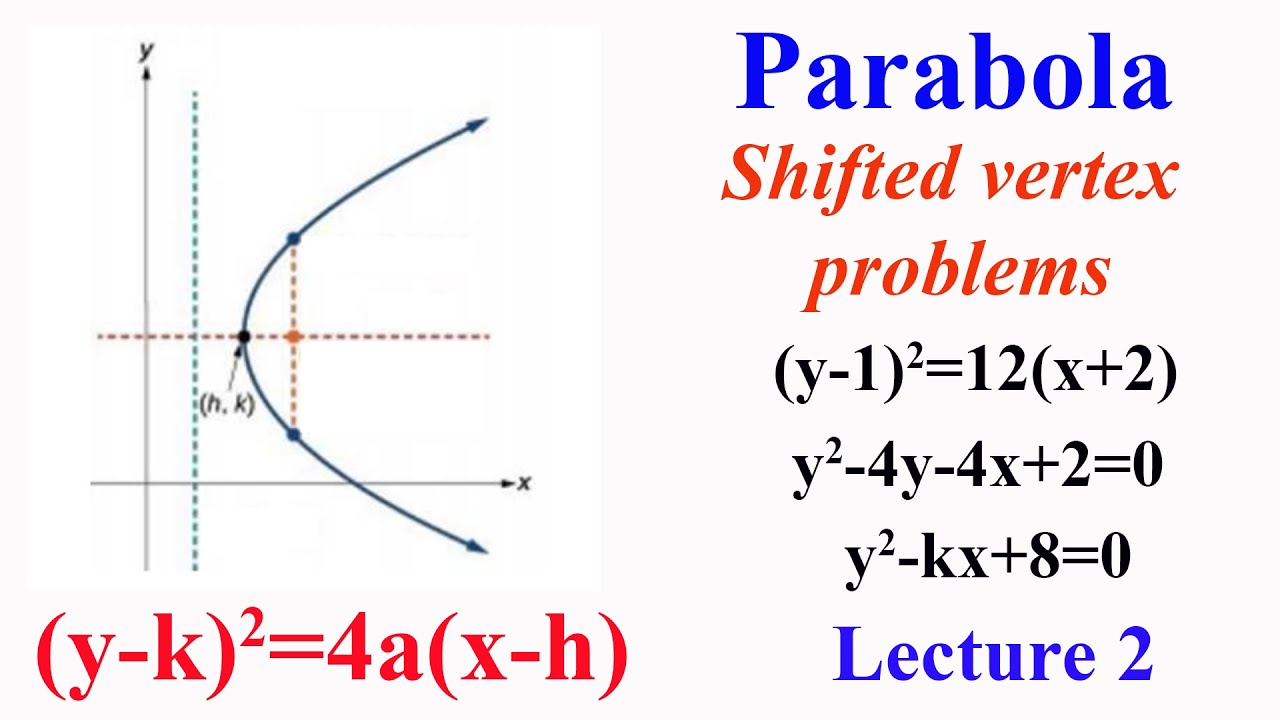



Parabola Lecture 2 Shifted Vertex Y K 2 4a X H With Examples Youtube
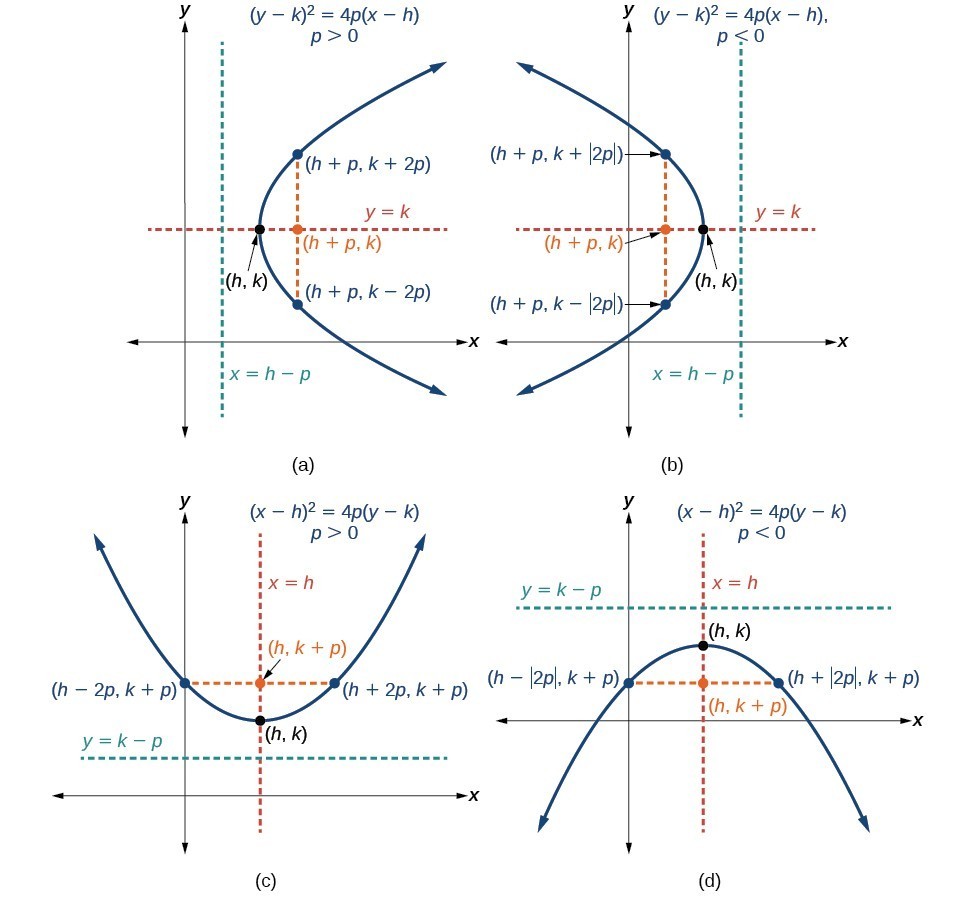



Parabolas With Vertices Not At The Origin College Algebra




Chapter 8 1 Conic Sections Parabolas Honors Pre Calculus Rogers High School Pdf Free Download



3




3 A Find An Equation Of The Parabola X H Chegg Com




Parabolas Andymath Com




Equation Of Parabola Directrix Focus Axis Problems With Solutions




The Parabola Precalculus Ii
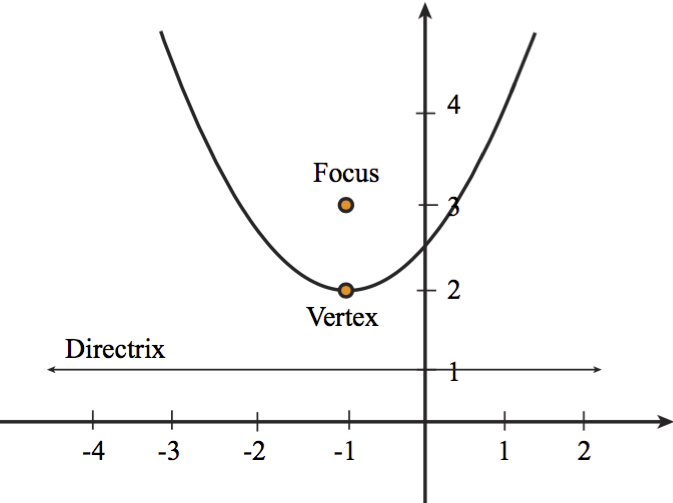



Conic Sections Conic Form Of A Parabola



Conic Sections Parabolas Summary Analysis Sparknotes
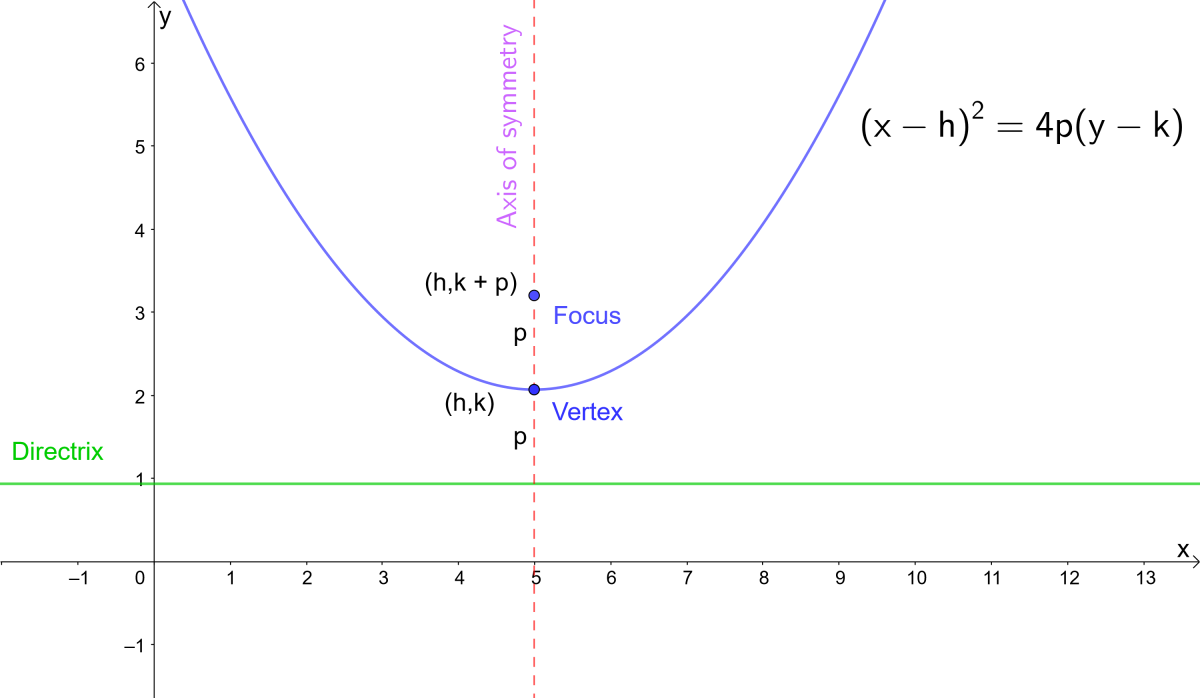



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation
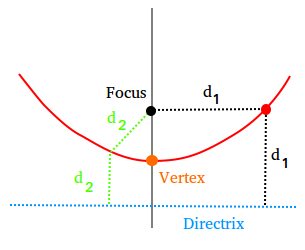



Parabola Definition And Equation



0 件のコメント:
コメントを投稿