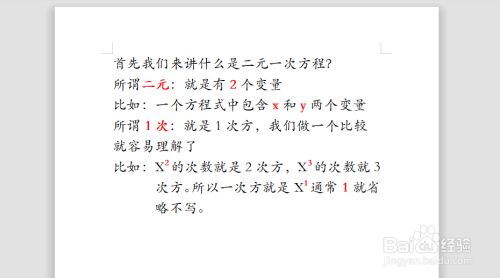
若知道某一元二次方程式的兩根,我們能不能反推而求得這個一元二次 方程式呢? 設α、β為所求方程式ax bx c2 =0的兩根。 等號兩邊同除以a,得 2 0 bc xx aa = 由根與係數的關係得知: b a αβ =− 、 c a αβ= 因此,方程式可以改寫成xx2 −()αβ αβ=0。例如方程式2x3y=5的其中一個解為x=1,y=1,因為2*13*1=5 二元一次方程式在直角坐標平面上的圖形 因為二元一次方程式的解都是x=?,y=?,於是把x的值跟y的值用坐標來表示 例如上面的例子中得2x3y=5的一解為x=1,y=1,用坐標表示為(1,1),再把坐標標在坐標平面上2 2 次の の中で 2元1次方程式 を成り立たせる、x, y の組を選びなさい。 ① 2元1次方程式 が成り立つようなx, y の組を 求め、表の空欄をうめなさい・ ② 2元1次方程式 が成り立つようなx, y の組を 求め、表の空欄をうめなさい・ ③ ① 、② をもとにして、連立
Search Q E4 Ba 8c E5 85 E4 B8 80 E6 Ac A1 E6 96 B9 E7 A8 8b E5 85 Ac E5 8f Tbm Isch
2元1次方程式计算机
2元1次方程式计算机-線形代数i 第4回 1 2 連立1次方程式の解法 線形代数の重要な応用例の一つが、連立1次方程式の解法である。この章では、連立1次方程式の系 統的な解法を考察することにより、線形代数の有用性と強さを練習問題9 任意の連立2元1次方程式をCramerの公式で解くプログラムを作れ。方程式の各 係数と定数項をキーボードから入力出来るようにし、次の連立方程式を解け。 (4x1 5x2 = 14 8x1 28x2 = 64 (念のための解答x1 = 1, x2 = 2) 52 Gaussの消去法 n元の連立1次方程式は




二元一次方程式與直線的關係 106學年高職數學 B 第一冊 發現學習的美麗新世界
よって、2元2次方程式といいます。解は式=0の時のxとyの値を求めます。 (3)の式の説明 未知数はxが1つあるので1元、xは1乗と2乗で一番大きい乗数は2乗なので2次。 よって、1元2次方程式といいます。解は式=0の時のxの値を求めます。 この様に、2次方程式に已知一個三元一次的聯立方程式,如下所示:保留係數為 0 的各項是為方便後面的工作。 10x 5 E27x 6 2x 7 L F9 28x 50x 6 4x 7 L226 35x 5 9x 60x 7 L F3 本實驗的聯立方程式如果叫你們用紙筆算,可能都會為了下課而不擇手段。還好實驗室裡有 電腦的EXCEL 軟體可供使用。我們的本意是解方程式(1)。但是如果能事先解出方程式(3), 原來的方程式也就迎刃而解。因此方程式(3)叫做方程式(1)的預解方程式, 簡稱預解式。利用 Lagrange 預解式的方法,讓我們試試看如何解四次方程式 x 4 ax 3 bx 2 cxd=0 。令 ,,, 為其四根。
今回から、2次方程式を見ていく。 まずは、2次方程式の解き方から始めよう。 前回 ←平方根の補充問題(難) 次回 →2次方程式の解き方(2)(展開、置き換え、二乗の利用)(標) 31 2次方程式の解き方 311 基本的な2次方程式の解き方(1)(基) 312 2次方程式のの解き方(2)(展開・置き換え・二P7~ 2元1次連立方程式・3元1次連立方程式 Class No Name Exercise 6 次の連立方程式を解きなさい. (1) € xy−3z=−10 x−y2z=11 2xy−z=3 ⎧ ⎨ ⎪ ⎩ ⎪ 連立方程式の各式を,上から順に ① , ② , ③2元連立1次方程式 樋口さぶろお https//hig3net 龍谷大学理工学部数理情報学科 線形代数L07() 最終更新 Timestamp " Tue 1013 JST hig" 今日の目標 行列の行基本変形が説明できる高橋線形x31 行列の行基本変形で, 解なし, 不定も含め, 連立
この映像授業では「中2 数学 1次関数11 2元1次方程式2」が約4分で学べます。問題を解くポイントは「ラッキーパターン!計算バグ (入力値と間違ってる結果、正しい結果、参考資料など) 説明バグ (間違ってる説明文と正しい説明文など) アンケートは下記にお客様の声として掲載させていただくことがあります。 2元1次方程式(axby=p,cxby=qの法則) にリンクを張る方法X, y を未知数とする 連立2元1次方程式 (simultaneous linear equations with two unknowns) { a 1 x b 1 y = c 1 a 2 x b 2 y = c 2 の解を求めるために、未知数 x, y の一方を消去します。 まずは、 x を求めるために y を消去します。



七年级下 数学实际问题与二元一次方程组题型归纳 含练习题答案 七年级 老杨的博客




二次方程 维基百科 自由的百科全书
ホーム >> カテゴリー分類 >> 行列 >> 線形代数 >>多元1次方程式の解(行列式を用いた表示) 学生スタッフ作成 初版:09年10月31日,最終更新日: 12年10月31日 2元1次方程式とは x2y = 9 x 2 y = 9 このように、 2 2 種類の文字の項がある 1 1 次式を、方程式と見た場合 2 2 元 1 1 次方程式といいます。 ※関数とみれば 1 1 次関数(次の章で学びます)です。 あまり言葉にこだわる必要はありません。 等式の変形をすることで x2y = 9 x 2 y = 9 2y = −x 9 2 y = − x 9 y =− y = − 1 2 1 2 x x 9 2 9 2本词条由 "科普中国"科学百科词条编写与应用工作项目 审核 。 只含有一个 未知数 (一元),并且未知数项的最高 次数 是2(二次)的 整式方程 叫做一元二次方程 。 一元二次方程经过整理都可化成一般形式ax²bxc=0(a≠0)。



21 6 1 二元二次方程组的解法 哔哩哔哩 Bilibili



二元一次方程组练习题精选 附答案 职场达人网 职场知识 职场礼仪 职场法则
將二元一次聯立方程式中的方程式 (1)或(2),利用等量公理做運算之後即方程式(1)或(2)各乘某些倍數之後,可使方程式(1)與(2),相加或相減之後,變成一元一次方程式來解題,進而求得聯立方程式的解,我們稱為 加減消去法 。(1元)1次方程式・・・・・1つの文字だけ(例えば x)の方程式 解く手順 (1)方程式の中にカッコがあれば、それをはずす (2)係数(単項式の数の部分)が分数や少数のときは、両辺に適当な数をか2元連立1 次方程式の簡便解法 2 解の分母 まず,連立方程式①と②の左辺の係数だけを抜き出して というものをつくります。 このように,数や文字を縦,横に並べたものを行列(matrix:メイト リクス(発音注意))といいます。



二元一次方程组练习题60道 含答案 教育资讯 娱乐新闻网



代入法解二元一次方程组练习题 松鼠文库
本词条由"科普中国"科学百科词条编写与应用工作项目审核。 含有两个未知数,并且含有未知数的项的次数都是1的整式方程叫做二元一次方程。 所有二元一次方程都可化为axbyc=0(a、b≠0)的一般式与axby=c(a、b≠0)的标准式,否则不为二元一次方程。 但是,若在平面直角坐标系中,例如直线方程"x=1",直线上每一个点的横坐标x都有与其相对应的纵坐标y,这种 列成方程式為 繼續化簡 (3)列成方程式為 繼續化簡 由例題771可知,生活中有很多情境是可以列成一元二次方程式的。 接著我們再來看看什麼是一元二次方程式的解。 元一次方 4102 程所以a不能等于0 求根公式为 1653 :x1=(b(b^24ac)^1/2)/2a ,x2=(b(b^24ac)^1/2)/2a 扩展资料 韦达定理说明了一元二次方程中根和系数之间的关系。 法国数学家弗朗索瓦·韦达于1615年在著作《论方程的识别与订正》中建立了方程根与系数的




高数 二元一次微分方程组求解问题 雨露学习互助




二元一次方程 组 含参问题 每日头条
N 元連立1 次方程式 m n 行列の簡約化 行列の行基本変形 m n 行列で 操作I(i,a) i 行目に定数a をかける(a ̸= 0) 操作II(i,j,b) i 行目にj 行目のb 倍を加える 操作III(i,j) i 行目とj 行目を入れ替える https//bitly/rrmatrix (全学認証)高橋線形定理41 拡大係数行列に行基本変形を行っても, 対応する連立1次方程式如果有一位小數與二位小數混合時,你就應該同乘以 ,為了是讓二次小數變成整數。下面這個習題就讓同學們嘗試看看這樣的做法。 習題 解一元一次方程式 () = 。補講12 連立2元1次方程式の解法 1 はじめに 本補講では,連立2元1次方程式の解の公式に相当するものを紹介します。 以下の議論は文字式だけによるもの,つまり代数的なものです。それゆえこう いった扱いに慣れていないものにとっては,かなり さくそう



2元1次方程教学 西瓜视频搜索




第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download
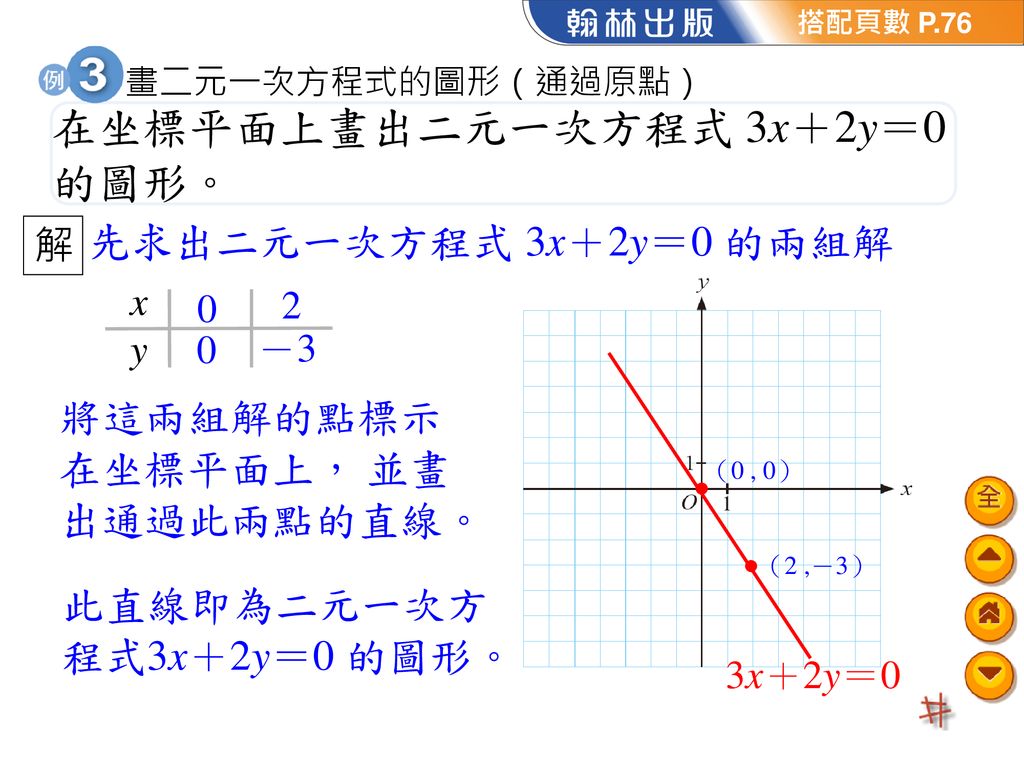
問題探索2 O 1 1 y x 事實上,方程式 2x-y=1 的解都會落在直線 M 上;而在直線 M 上的任一 點,其坐標都是方程式 2x-y=1 的解,所以方程式 2x-y=1 在坐標平面上的 圖形就是直線 M。 74 第2 章 直角坐標與二元一次方程式的圖形 1下22三校indd 74 8 下午 81次方程式を解くとは 3x5=−1 (1) のように未知数 x を含む等式を x についての方程式といいます。 この頁では、1次方程式から「等式の性質」を使って解を求める方法を学びます。 x=··の形をした式を解といいます。2元1次不定方程式特殊解の簡便法による求め方 ~互除法を用いたシミュレート (順行 )簡便法について 札幌旭丘高校 中村文則 ユークリッドの互除法は,最大公約数を求める高速アルゴリズムである.応用として簡便法を用い二元一次



怎么解二元一次方程组 百度经验




2 二元一次方程式的圖形畫法 基本觀念 國一下2 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube
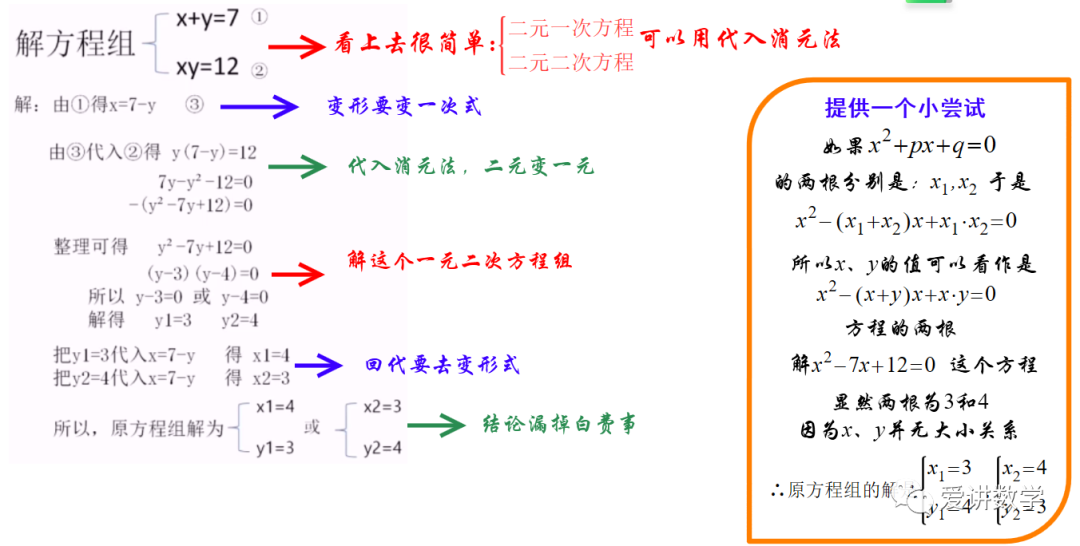
解二元一次聯立方程式時,一般我們希望能像例 2 中用 x=2y,或例 3 中 用 y =3-9 x 直接代入方程式求解;但若不是這樣,此時可以先整理方程式,將 其中一個方程式寫成 x = cy + d 或 y = ax + b 的樣子,再以代入消去法求聯立方




高二高中數學的 高二數學 二元一次不等式筆記 Clear




二元一次聯立方程式公式解 1下數學 魔術方塊and數學 隨意窩xuite日誌




二元一次方程 二元一次方程的解和圖像 請觀看更新版 Youtube



初一数学第八章二元一次方程组二元一次方程组应用题练习 初一数学 中考网




初二数学上册知识点 二元一次方程 教育频道 手机搜狐



H Puln4gl8 Dmm




如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl




二元一次方程组的解法提出了这条定理




专题09 二元一次方程组及其应用 教师版 备战21年中考数学专题复习精讲精练 七七文库www 77wenku Com



方程初中名师总结二元一次方程应用题 13种经典习题 都是干货 安安股票网



7 2 二元一次方程组的解法 Page27 华师大版七年级数学下册电子课本 教材 教科书 好多电子课本网




08一次函数与方程二元一次方程组初中数学初二 Youtube



小学二元一次方程练习题2 松鼠文库



C 编程求解二元二次方程组 特殊二元二次方程组的解法 2 David Rand的博客 Csdn博客




2 3二元一次方程组及其解法




1 1建立二元一次方程组 课后作业 含答案详解 Doc 豆知网




8 4三元一次方程组的解法课课练习及答案 Pdf版 Pdf 文档分享网



Excel求解多元一次 一元二次方程组就是这么简单 知乎




二元一次方程组练习题不会 来看看二元一次方程组知识点 每日头条




怎么解二元一次方程组 百度经验




01二元一次方程组的概念二元一次方程组初中数学初二 Youtube




有分数的二元一次方程怎么解 求分数的二元一次方程解法过程 三人行教育网 Www 3rxing Org




初二数学 二元一次方程组 测验卷 基础好的学生可争取满分 网易订阅
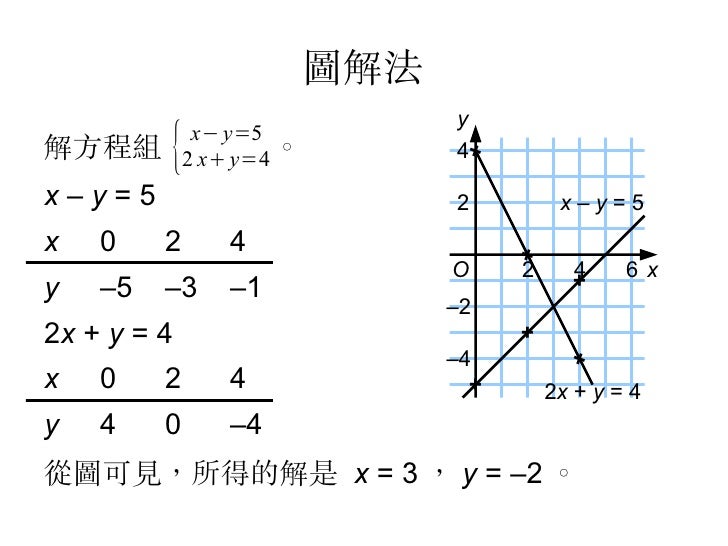



複習 二元一次方程及百分法




二元一次方程计算题及答案 豆知网




二元一次方程解法



二元一次方程组应用题经典题 附答案 职场达人网 职场知识 职场礼仪 职场法则



二元一次方程组练习题精选 附答案 职场达人网 职场知识 职场礼仪 职场法则



100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




初中数学 二元一次方程组经典试题解题步骤 含答案 必须收藏




复习专题 解析二元一次方程知识点及应用 知乎



二元一次方程组的8个类型 专治各种不会做的应用题




2元一次方程式公式解怎么解二元一次方程 組 百度經驗翻譯此網頁 Vexcil
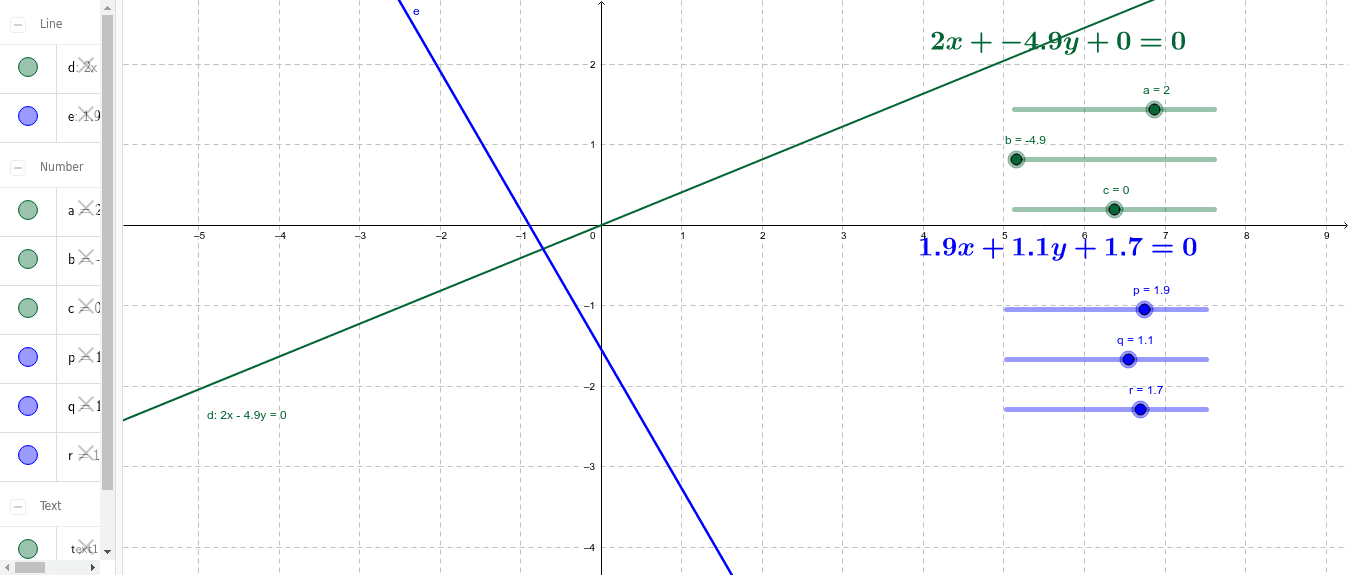



二元一次方程式圖形 Geogebra




二次方程 维基百科 自由的百科全书



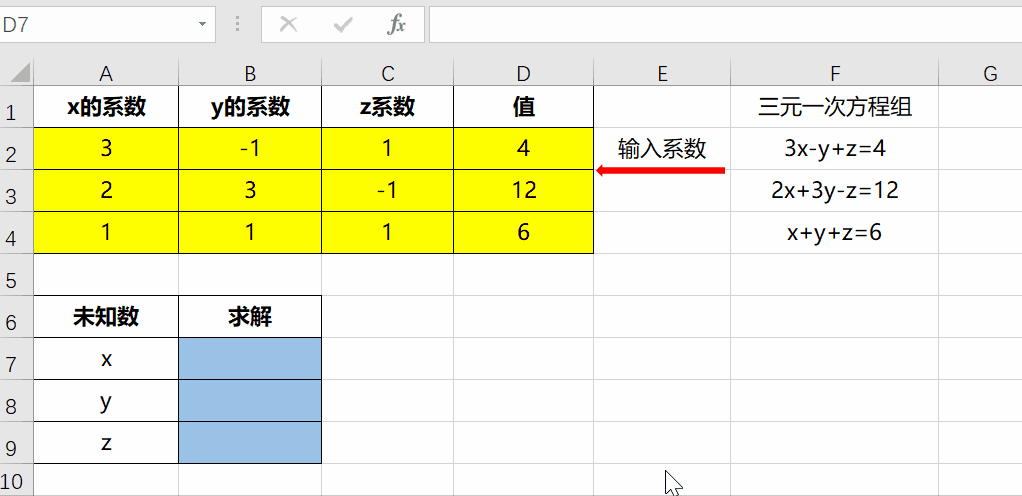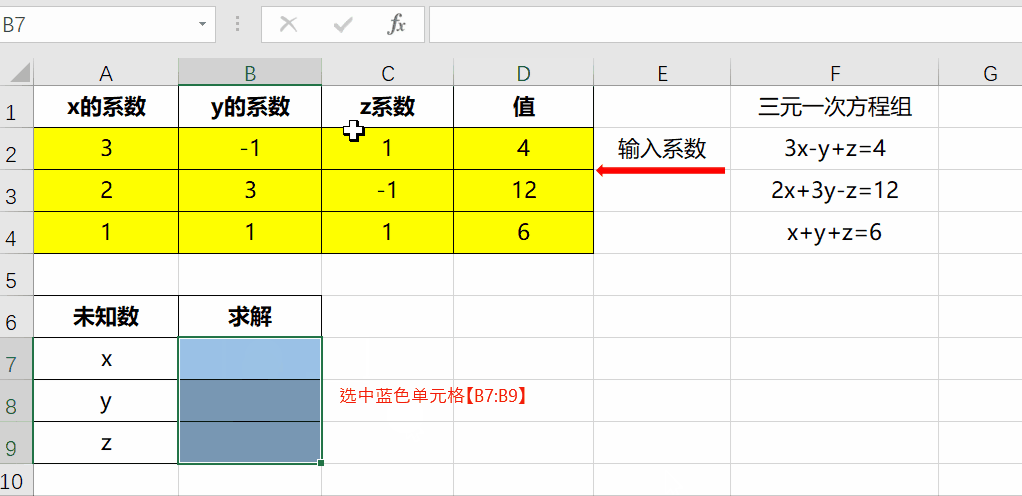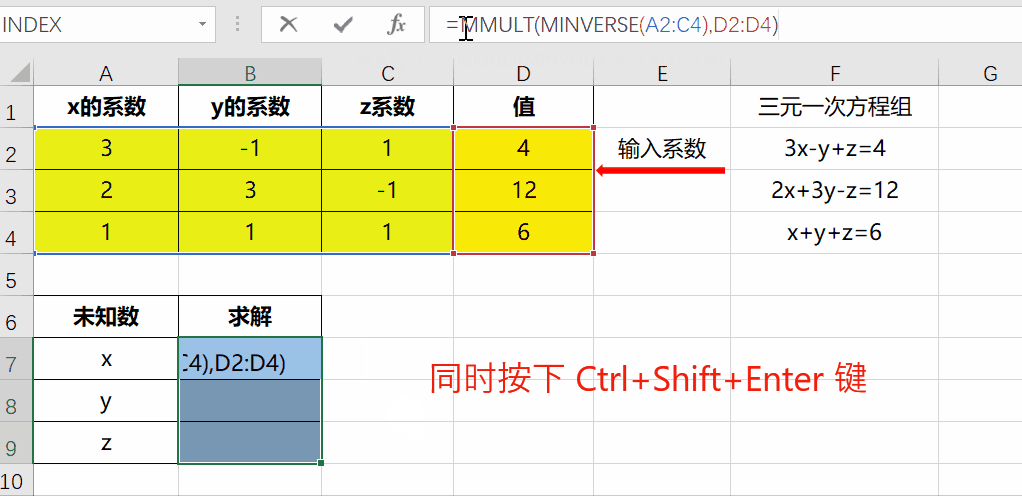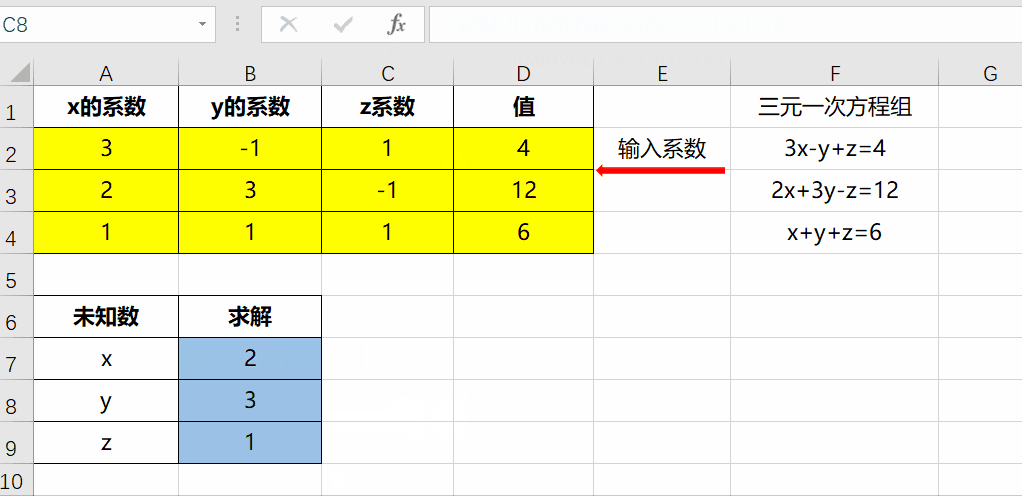
在excel中求解二元一次方程组 公式




Excel求解多元一次 一元二次方程组就是这么简单 知乎



1 二元一次方程组的矩阵形式 人教版高中选修4 2数学电子课本 数九网




怎么解二元一次方程组 百度经验




二元一次方程式的解 Youtube




年中考数学必考点练习 二元一次方程组 三好网



加减消元法解二元一次方程组 禾教 初中数学互动课堂



二元一次方程组练习题精选一 初三数学 中考网




如何用图示展示一个二元一次方程



悟空问答 计算二元一次方程组 计算又慢正确率又很低 怎么办 8个回答



二元一次方程 搜狗图片搜索




解二元一次方程 典型解答题的分析方法及切入点 每日头条



課程介紹 二元一次聯立方程式 發現學習的美麗新世界
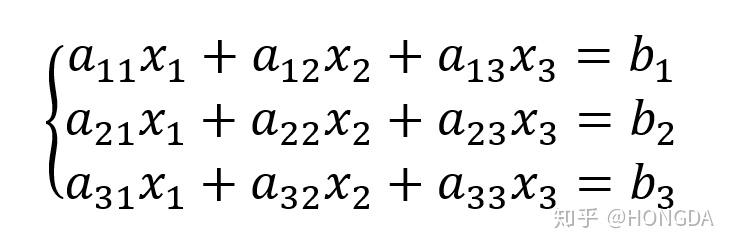



关于线性代数三阶行列式运算法则的推导 二 知乎



二元一次方程组练习题精选 附答案 职场达人网 职场知识 职场礼仪 职场法则



沪科版数学八年级 二元一次方程组的图象解法 同步练习 数学练习题 合肥中考网




二元一次方程式題型 大家都在找解答 訂房優惠報報




解二元一次方程的步骤解二元一次方程组 详细过程




例題 解二元一次聯立方程式 綜合應用1 解二元一次聯立方程式 均一教育平台



二元一次方程组 第2课 用代入法解二元一次方程组 二元一次方程组 第2课 用代入法解二元一次方程组资料 新学语文网




1对3春季数学6年级第11讲二元一次方程组




二元一次方程組 二元一次方程組是指含有兩個未知數 X和y 並且所含未知 百科知識中文網




学生在解二元一次方程组中常犯的错误 每日头条



实际问题与二元一次方程组应用题归纳 整理 松鼠文库




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



二元一次方程各类应用题 松鼠文库




二元一次方程组及其解法专题总结 楠木轩



二元一次方程 台灣word




C 求二元一次方程解 Luojie1011的博客 Csdn博客




如何用图示展示一个二元一次方程




人教七下数学 8 2消元 解二元一次方程组 练习题 附答案 七七文库www 77wenku Com



二元一次方程组第三单元自测 初一数学辅导 初中数学 学习资料大全 免费学习资源下载



Search Q E4 Ba 8c E5 85 E4 B8 80 E6 Ac A1 E6 96 B9 E7 A8 8b E7 E4 B9 A0 E9 98 Tbm Isch



二元一次方程组练习题100道 松鼠文库



二元一次方程经典例题讲解 松鼠文库



1



3元1次方程的解法daan 关于3元1次方程组的解法答案



二元一次方程解题时常见思路或方法 掌握后基本都是送分的题目 哔哩哔哩 つロ干杯 Bilibili




二元一次方程式與直線的關係 106學年高職數學 B 第一冊 發現學習的美麗新世界



Search Q E4 Ba 8c E5 85 E4 B8 80 E6 Ac A1 E6 96 B9 E7 A8 8b E5 85 Ac E5 8f Tbm Isch



二元一次方程组练习题100道 松鼠文库




翻轉學習影片 國中 數學 4 2 2 解二元一次聯立方程式



1




Matlab求解二元一次方程组的解得表达式 Havihouston 博客园



100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



二元一次方程 搜狗图片搜索




ひどい2 元1 次方程式 壁紙配布




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



七年级数学下册第8章二元一次方程组同步练习及答案 8 4三元一次方程组的解法 2 初中数学 学习资料大全 免费学习资源下载



如何解二元一次方程式如何解二元一次方程 百度經驗 Qaxnl




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




如何用matlab求解二元一次方程 并且解有可能是复数 Csdn社区
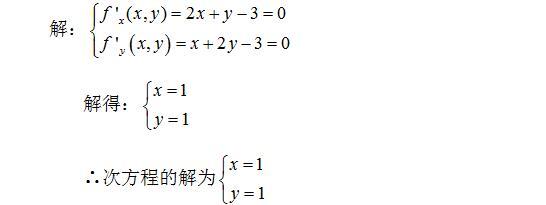



二元二次方程的解法 知乎




畫出二元一次方程式的圖形 Youtube




2元1次方程式 無料で使える中学学習プリント



3元1次方程的解法daan 关于3元1次方程组的解法答案




初二二元一次方程試題類型 每日頭條



0 件のコメント:
コメントを投稿